訳者序
一九〇九年、レオン・ワルラスの七十五歳の
 daillon を作った。それには、次の銘が刻んである。
daillon を作った。それには、次の銘が刻んである。"A L
 on Walras, n
on Walras, n
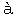 Evreux en 1834, professeur
Evreux en 1834, professeur 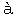 l'Acad
l'Acad mie et
mie et 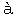 l'Universit
l'Universit de Lausanne, qui le premier a
de Lausanne, qui le premier a  tabli les conditions g
tabli les conditions g n
n rales de l'
rales de l' quilibre
quilibre  conomique, fondant ainsi l'
conomique, fondant ainsi l' cole de Lausanne. Pour honorer cinquante ans de travail d
cole de Lausanne. Pour honorer cinquante ans de travail d sint
sint ress
ress ."
."(一八三四年に Evreux に生れローザンヌ Acd
 mie 並びにローザンヌ大学の教授であり、経済均衡の一般的条件を論証した最初の人であり、ローザンヌ学派の開祖であるレオン・ワルラスに。利慾を離れた五十年の研究生活に敬意を表するために。)
mie 並びにローザンヌ大学の教授であり、経済均衡の一般的条件を論証した最初の人であり、ローザンヌ学派の開祖であるレオン・ワルラスに。利慾を離れた五十年の研究生活に敬意を表するために。)この銘こそはワルラスの学問的業績を最も明確に表明しているものである。多くの経済学説史家は、メンガー、ジェヴォンスと共に限界利用説を作りあげたこと、または数学を経済学に応用したことをもって、ワルラスの学問的功績となそうとしている。まことにこの点に関するワルラスの業績は、時間的に見ればジェヴォンスとメンガーとに
 pendance)を認識した点にある。一切の経済現象は各々独立なものではなく、相互に密接に作用し合っている。これら経済現象中のいずれの一つに起る変化も他のすべてに影響を及ぼし、これらの影響はまた逆にこの一つの現象に影響を及ぼす。従って経済現象は
pendance)を認識した点にある。一切の経済現象は各々独立なものではなく、相互に密接に作用し合っている。これら経済現象中のいずれの一つに起る変化も他のすべてに影響を及ぼし、これらの影響はまた逆にこの一つの現象に影響を及ぼす。従って経済現象は ciproquement)決定し合うことを証明した最初の人がワルラスであったことは、争う余地がない(二)。ところで、この相互依存の関係を明らかにするには、パレートがいっているように、通常の論理は無力であり、数学の力に
ciproquement)決定し合うことを証明した最初の人がワルラスであったことは、争う余地がない(二)。ところで、この相互依存の関係を明らかにするには、パレートがいっているように、通常の論理は無力であり、数学の力にこの残滓はパレートによって除き去られて、ワルラスの一般均衡理論は、後期ローザンヌ学派の純粋なる一般均衡理論となった。今日 d
 sint
sint ress
ress の経済科学者にとっては、主観的価値説もなければ、労働価値説もない。ひとり一般均衡理論あるのみである。経済現象の d
の経済科学者にとっては、主観的価値説もなければ、労働価値説もない。ひとり一般均衡理論あるのみである。経済現象の d sint
sint ress
ress な研究をなそうと志す人々は、ワルラスとパレートとの研究から始めねばならない。誤訳なども多くあるかもしれないこの「純粋経済学要論」が、これらの人々にとっていくらかの役に立ち得るならば、訳者のこの仕事は無駄にはならぬであろう。この場合にも、R. Gibrat が Les In
な研究をなそうと志す人々は、ワルラスとパレートとの研究から始めねばならない。誤訳なども多くあるかもしれないこの「純粋経済学要論」が、これらの人々にとっていくらかの役に立ち得るならば、訳者のこの仕事は無駄にはならぬであろう。この場合にも、R. Gibrat が Les In galit
galit s
s  conomiques, Paris. 1931. の表紙に引用した Carver の一句は、記憶のうちに止めらるべきであろう。
conomiques, Paris. 1931. の表紙に引用した Carver の一句は、記憶のうちに止めらるべきであろう。"The author hopes that the reader who takes up this volume may do so with the understanding that economics is a science rather than a branch of polite literature, and with the expectation of putting as much mental effort into the reading of it as he would into the reading of a treatise on physics, chemistry, or biology.(四)"
この飜訳に際しても、「国際貿易政策思想史研究」の場合と同様に、高垣寅次郎先生の御指導と御尽力を
一九三三年三月
手塚壽郎
註一 Sensini: La teoria della "rendita," 1912, pp. 407-8.
註二 〔Antonelli: Le'on Walras, dans la Revue d'histoire des doctrines e'conomiques et sociales, 1910, p. 187.
註三 〔V. Pareto: Manuel d'e'conomie politique trad. de l'italien par Al. Bonnet, 1909. pp. 160, 247.
註四 T. N. Carver: The Distribution of Wealth, 1899, Preface.
[#改ページ]凡例
一 この書物は、L
 on Walras: El
on Walras: El ments d'
ments d' conomie politique pure ou Th
conomie politique pure ou Th orie de la richesse sociale. Paris et Lausanne. を、一九二六年版に拠って、訳出したものである。厳密に訳せば、書名は「純粋経済学要論||社会的富の理論」とせられねばならぬのではあるが、称呼上の簡便を期するため、単に「純粋経済学要論」としておいた。一九二六年版は、三箇所に加えられた僅少の修正を除けば、決定版として知られている第四版すなわち一九〇〇年版と異る所が無い。これらのうち、二箇所はワルラスが一九〇二年付の註をもって一九二六年版に断っているが(本訳書下巻、第三二六、三六二節)、他の一箇所は断ってない。しかしこの一箇所は旧版の当該部分をより容易に理解せしめようとしてなされた修正であって、重要な修正ではない。第八二節がこの部分である。
orie de la richesse sociale. Paris et Lausanne. を、一九二六年版に拠って、訳出したものである。厳密に訳せば、書名は「純粋経済学要論||社会的富の理論」とせられねばならぬのではあるが、称呼上の簡便を期するため、単に「純粋経済学要論」としておいた。一九二六年版は、三箇所に加えられた僅少の修正を除けば、決定版として知られている第四版すなわち一九〇〇年版と異る所が無い。これらのうち、二箇所はワルラスが一九〇二年付の註をもって一九二六年版に断っているが(本訳書下巻、第三二六、三六二節)、他の一箇所は断ってない。しかしこの一箇所は旧版の当該部分をより容易に理解せしめようとしてなされた修正であって、重要な修正ではない。第八二節がこの部分である。二 原著の叙述は、ほとんど全部条件法を用い、原著者がその主張にいかに謙譲であったかをよく示している。だが訳文には、必要な場合のほか、大部分直接法を用いることとした。
[#改ページ]
レオン・ワルラスの略伝
レオン・ワルラス(Marie-Esprit-L
 on Walras)は、一八三四年十二月十六日、パリを西北に百
on Walras)は、一八三四年十二月十六日、パリを西北に百 loquence fran
loquence fran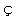 aise)の講師となった。一八四七年、学位論文 Le Cid, esquisse litt
aise)の講師となった。一八四七年、学位論文 Le Cid, esquisse litt raire によって、文学博士(Docteur-
raire によって、文学博士(Docteur-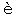 s-lettres)を授けられた。その後は視学官として、Nancy, Caen, Douai, Pau 等に転任している。これらの生活を通じてオーギュストが専門とした学問はフランス語学・文学・哲学であったのであるが、エヴルーの教師時代から経済学の研究が常に彼の大なる興味をひきつけていた。その間、かなり多数の経済学上の論文を公にしているのみならず、一八三一年には、「富の性質及び価値の源泉について」(De la nature de la richesse et de l'origine de la valeur. Paris.)を公刊し、一八四九年には「社会的富の理論、経済学の基本原理の要約」(Th
s-lettres)を授けられた。その後は視学官として、Nancy, Caen, Douai, Pau 等に転任している。これらの生活を通じてオーギュストが専門とした学問はフランス語学・文学・哲学であったのであるが、エヴルーの教師時代から経済学の研究が常に彼の大なる興味をひきつけていた。その間、かなり多数の経済学上の論文を公にしているのみならず、一八三一年には、「富の性質及び価値の源泉について」(De la nature de la richesse et de l'origine de la valeur. Paris.)を公刊し、一八四九年には「社会的富の理論、経済学の基本原理の要約」(Th orie de la richesse sociale, ou R
orie de la richesse sociale, ou R sum
sum des principes fondamentaux de l'
des principes fondamentaux de l' conomie politique. Paris.)を公刊している。これらの二書は、レオンの思想に重大な影響を及ぼしたものとして、重要視すべきものである。レオン自身もこのことを認めている(二)。単に価値の心理的観方をなした点においてのみならず、また経済学を数理的科学でなければならぬと考えた点においても、父の思想はそのままレオンの思想となっているのである(三)(四)。
conomie politique. Paris.)を公刊している。これらの二書は、レオンの思想に重大な影響を及ぼしたものとして、重要視すべきものである。レオン自身もこのことを認めている(二)。単に価値の心理的観方をなした点においてのみならず、また経済学を数理的科学でなければならぬと考えた点においても、父の思想はそのままレオンの思想となっているのである(三)(四)。レオンは、一八五一年、文科大学入学資格者(Bachelier
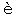 s lettres)となり、一八五三年、理科大学入学資格者(Bachelier
s lettres)となり、一八五三年、理科大学入学資格者(Bachelier 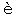 s sciences)となり、砲工学校(Ecole Polytechnique)の入学試験を受けたが、失敗した。この頃彼は微積分学や理論力学を勉強していたが、それのみでなく、クールノーの「富の理論の数学的原理に関する研究」(Recherches sur les principes math
s sciences)となり、砲工学校(Ecole Polytechnique)の入学試験を受けたが、失敗した。この頃彼は微積分学や理論力学を勉強していたが、それのみでなく、クールノーの「富の理論の数学的原理に関する研究」(Recherches sur les principes math matiques de la th
matiques de la th orie des richesses. 1838.)をも初めて読んだという(五)。一八五四年、鉱山学校(Ecole des Mines)に入学したが、まもなく退学して、文学などに熱中した。
orie des richesses. 1838.)をも初めて読んだという(五)。一八五四年、鉱山学校(Ecole des Mines)に入学したが、まもなく退学して、文学などに熱中した。一八五八年、レオンは小さな小説 Francis Sauveur を公にしている。しかし父は彼に経済学の勉強を熱心にすすめた。レオンが経済学者として立つに至るべき動機はここに発すると、彼自らいっている。「私の全生涯の最も決定的な時は、一八五八年の夏のある美しい夜であった。その夜 Gave de Pau 河の河辺を散歩していたとき、父は、一九世紀中になさるべき二つの大なる仕事||歴史を書き上げることと、社会科学を建設すべきこと||が残っていることを力説した。これらの二つの仕事のうちの第一については、ルナン(Renan)が充分に父を満足せしめるであろうことを、父は知らなかった。第二の仕事は、父が終生念願していた所であり、この仕事に特に父は感激をもっていた。父は、私がこの仕事を継ぐべきであると、力強くいっていた。Les Roseaux という農場の入口まで来たとき、私は、文学や文芸批評を放擲して、父の仕事を
一八五九年に、レオンは Journal des Economistes の記者となり、一八六〇年に、Presse の記者となった。まもなくこれをもやめた。この年「経済学と正義、プルードンの経済学説の吟味と駁論」(L'Economie politique et la justice. Examen critique et r
 futation des doctrines
futation des doctrines  conomiques de M. P.-J. Proudhon. Paris.)を公にした。また同年七月、ローザンヌに開かれた国債租税会議に列席した。また同年ヴォー(Vaud)州が募集した租税に関する懸賞論文に応じた。一八六一年に出版された「租税理論批判」(Th
conomiques de M. P.-J. Proudhon. Paris.)を公にした。また同年七月、ローザンヌに開かれた国債租税会議に列席した。また同年ヴォー(Vaud)州が募集した租税に関する懸賞論文に応じた。一八六一年に出版された「租税理論批判」(Th orie critique de l'imp
orie critique de l'imp t. Paris.)がそれである。プルードンの「租税理論」(Th
t. Paris.)がそれである。プルードンの「租税理論」(Th orie de l'imp
orie de l'imp t. Paris.)が第一等賞となり、レオンは第四等となった。
t. Paris.)が第一等賞となり、レオンは第四等となった。レオンは一八六五年に至るもなお一定の職業を得なかったが、この頃
 on Say と共にこの運動の週刊雑誌「労働」(Le Travail)を発刊した。ひとたびこの雑誌に公にされた一八六七年と八年の公開講演「社会理想の研究」(Recherche de l'id
on Say と共にこの運動の週刊雑誌「労働」(Le Travail)を発刊した。ひとたびこの雑誌に公にされた一八六七年と八年の公開講演「社会理想の研究」(Recherche de l'id al social)は一八六八年、単行書として出版された。その後銀行員となったりしているうちに、一八七〇年六月、レオンはルイ・リュショネー(Louis Ruchonnet)の来訪を受けたが、氏は近くローザンヌ大学に経済学講座が開設せられるべきことを報じ、かつその教授候補者となることをレオンにすすめた。レオンはこのすすめに応じ、この受験準備のため、八月七日ノルマンディーに赴き、静かな環境のうちに勉強した。試験官は州の名士三名と経済学者四名から成っていた。これら三人の名士はワルラスの採用に賛成したが、四人の経済学者のうち三人はこれに反対した。残る一人であるジュネーヴ大学教授であった経済学者ダメト(Dameth)は、ワルラスの数理経済学を正しいとは思わないが、しかしかような思想を発展せしめ講義せしめてみるのは、学問の進歩のために有益であろうといって、ワルラスの採用に賛成した。その結果、ワルラスはローザンヌ大学の教授に任命せられ、同年十二月十六日開講した。この時から、一八九二年にパレートが彼の講座を継ぐまで、ワルラスは数理経済学の建設に全努力を傾倒した。その間、一八七三年にまず「交換の数学的理論の原理」(Principes d'une th
al social)は一八六八年、単行書として出版された。その後銀行員となったりしているうちに、一八七〇年六月、レオンはルイ・リュショネー(Louis Ruchonnet)の来訪を受けたが、氏は近くローザンヌ大学に経済学講座が開設せられるべきことを報じ、かつその教授候補者となることをレオンにすすめた。レオンはこのすすめに応じ、この受験準備のため、八月七日ノルマンディーに赴き、静かな環境のうちに勉強した。試験官は州の名士三名と経済学者四名から成っていた。これら三人の名士はワルラスの採用に賛成したが、四人の経済学者のうち三人はこれに反対した。残る一人であるジュネーヴ大学教授であった経済学者ダメト(Dameth)は、ワルラスの数理経済学を正しいとは思わないが、しかしかような思想を発展せしめ講義せしめてみるのは、学問の進歩のために有益であろうといって、ワルラスの採用に賛成した。その結果、ワルラスはローザンヌ大学の教授に任命せられ、同年十二月十六日開講した。この時から、一八九二年にパレートが彼の講座を継ぐまで、ワルラスは数理経済学の建設に全努力を傾倒した。その間、一八七三年にまず「交換の数学的理論の原理」(Principes d'une th orie math
orie math matique de l'
matique de l' change)が公にせられ、一八七五年に「交換の方程式」(Equations de l'
change)が公にせられ、一八七五年に「交換の方程式」(Equations de l' change)が、一八九六年に「生産の方程式」(Equations de la production)及び「資本化の方程式」(Equations de la capitalisation)が公にせられ、それらが綜合せられて「純粋経済学要論」(El
change)が、一八九六年に「生産の方程式」(Equations de la production)及び「資本化の方程式」(Equations de la capitalisation)が公にせられ、それらが綜合せられて「純粋経済学要論」(El ments d'
ments d' conomie politique pure)の第一版第一分冊が一八七四年に、第二分冊が一八七七年に出版せられ、第二版が一八八九年に、第三版が一八九六年に出版せられた。これら出版の事情と各版の相異とは原著第四版の序文に明らかにせられている。これらの相異のうち、貨幣の価値に関する第一版と第二版とのそれは、我々の注意に値するものであろう。マージェット(A. W. Marget)が指摘しているように、第一版に見られるフィッシャー流の貨幣数量説は、第二版においてケンブリッジ学派の数量説に変化しているのである(七)。
conomie politique pure)の第一版第一分冊が一八七四年に、第二分冊が一八七七年に出版せられ、第二版が一八八九年に、第三版が一八九六年に出版せられた。これら出版の事情と各版の相異とは原著第四版の序文に明らかにせられている。これらの相異のうち、貨幣の価値に関する第一版と第二版とのそれは、我々の注意に値するものであろう。マージェット(A. W. Marget)が指摘しているように、第一版に見られるフィッシャー流の貨幣数量説は、第二版においてケンブリッジ学派の数量説に変化しているのである(七)。ローザンヌ大学を退いて後も、ワルラスの学問的活動は停止していない。一八九六年には論文集「応用経済学研究」(Etudes d'
 conomie appliqu
conomie appliqu e)を、一八九八年には論文集「社会経済学研究」(Etudes d'
e)を、一八九八年には論文集「社会経済学研究」(Etudes d' conomie sociale)を出版したほか、大小の論文を公にしている。
conomie sociale)を出版したほか、大小の論文を公にしている。翌年にはノーベル賞を目指して、著作を志している。一九〇七年の Questions pratiques de l
 gislation ouvri
gislation ouvri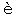 re et d'
re et d' conomie politique に公にされた論文「社会的正義と自由交換による平和[#「平和」は底本では「価格」、正誤表による訂正]」(La Paix par la justice sociale et le libre
conomie politique に公にされた論文「社会的正義と自由交換による平和[#「平和」は底本では「価格」、正誤表による訂正]」(La Paix par la justice sociale et le libre  change)はその一端であるという。
change)はその一端であるという。一九一〇年一月五日クララン(Clarens)に逝った。
註一 L. Walras: Un initiateur en  conomie politiqu
conomie politiqu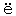 A. A. Walras, dans la Revue du mois, ao
A. A. Walras, dans la Revue du mois, ao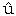 t 1908, p. 173.
t 1908, p. 173.
 conomie politiqu
conomie politiqu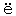 A. A. Walras, dans la Revue du mois, ao
A. A. Walras, dans la Revue du mois, ao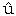 t 1908, p. 173.
t 1908, p. 173.註二 本書原著第四版の序、二一頁参照。
註三 E. Antonell Un
Un  conomiste de 1830: Auguste Walras, dans la Revue d'histoire
conomiste de 1830: Auguste Walras, dans la Revue d'histoire  conomique et sociale, 1923, p. 529.
conomique et sociale, 1923, p. 529.
 Un
Un  conomiste de 1830: Auguste Walras, dans la Revue d'histoire
conomiste de 1830: Auguste Walras, dans la Revue d'histoire  conomique et sociale, 1923, p. 529.
conomique et sociale, 1923, p. 529.註四 オーギュストとクールノーとの関係については、L. Hecht: A Cournot und L. Walras, Heidelberg, 1930, p. 23 以下を参照。
註五 Antonell L
L on Walras, dans la Revue d'histoire des doctrines
on Walras, dans la Revue d'histoire des doctrines  conomiques, 1910, p. 170. Cf. Bompair
conomiques, 1910, p. 170. Cf. Bompair Du Principe de libert
Du Principe de libert
 conomique dans l'
conomique dans l'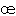 uvre de Cournot et dans celle de l'Ecole de Lausanne, p. 238.
uvre de Cournot et dans celle de l'Ecole de Lausanne, p. 238.
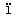 L
L on Walras, dans la Revue d'histoire des doctrines
on Walras, dans la Revue d'histoire des doctrines  conomiques, 1910, p. 170. Cf. Bompair
conomiques, 1910, p. 170. Cf. Bompair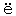 Du Principe de libert
Du Principe de libert
 conomique dans l'
conomique dans l'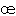 uvre de Cournot et dans celle de l'Ecole de Lausanne, p. 238.
uvre de Cournot et dans celle de l'Ecole de Lausanne, p. 238.註六 Antonell Principes d'
Principes d' conomie pure, pp. 24-5.
conomie pure, pp. 24-5.
 Principes d'
Principes d' conomie pure, pp. 24-5.
conomie pure, pp. 24-5.註七 A. W. Marget: L on Walras and the "Cash-Balance Approach" to Problem of the Value of Money, in the Journal of Political Economy, October 1931, pp. 569-600.
on Walras and the "Cash-Balance Approach" to Problem of the Value of Money, in the Journal of Political Economy, October 1931, pp. 569-600.
[#改ページ] on Walras and the "Cash-Balance Approach" to Problem of the Value of Money, in the Journal of Political Economy, October 1931, pp. 569-600.
on Walras and the "Cash-Balance Approach" to Problem of the Value of Money, in the Journal of Political Economy, October 1931, pp. 569-600.原著第四版の序
「純粋経済学要論」のこの第四版は最終版である(一)。一八七四年の六月、初版の巻頭に、私は今ここに転載しようとする次の文を書いた。
「一八七〇年、ヴォー州(Vaud)の参事院はローザンヌ大学の法学部に経済学の一講座の開設を計画し、かつその開設の準備として教授候補者を募った。私が今日あるのはこの見識ある発案の
「この概論は三部に
第一部 純粋経済学要論すなわち社会的富の理論。
第一編 経済学及び社会経済学の目的と分け方。第二編 交換の数学的理論。第三編 価値尺度財並びに貨幣について。第四編 富の生産及び消費の自然的理論。第五編 経済的進歩の条件と結果。第六編 社会の経済組織の諸形態の自然的必然的結果。
第二部 応用経済学要論すなわち農工商業による富の生産の理論。
第三部 社会経済学要論すなわち所有権と租税とによる富の分配の理論(二)。
「今ここに現われようとしているのは、第一巻の第一分冊である。これには、任意数の商品相互の交換の場合における市場価格決定の問題の数学的解法と需要供給法則の科学的方式とが含まれている。私がそこで用いた記号法は、当初には、やや複雑に見えるかもしれない。だが読者はこの複雑さに辟易してはならない。なぜなら、この複雑さは問題に内在して止むを得ないものであると同時に、このほかに難解な数学は少しも用いられていないから。ひとたびこれらの記号のシステムが理解せられれば、このことだけで、経済現象のシステムは自ら理解せられる。
「今から一ヵ月ほど前私は、マンチェスター大学の経済学教授ジェヴォンス氏が私の問題と同じ問題について書いた「経済学の理論」(The Theory of Political Economy)と題せられる著作が、一八七一年に、ロンドンマクミラン会社から出版せられているのを知った。だがそのときには私の第一分冊は全く稿を
「またジェヴォンス氏は特にこの新方法の一般的哲学的解説をなそうと努力し、かつこれを交換理論、労働理論、地代理論、資本理論へ応用すべき基礎を作ろうと努力している。私はこの分冊では特に交換の数学的理論を深奥な方法に拠って解説しようと努めた。だからジェヴォンス氏の方式の先駆性を認めねばならぬが、若干の重要な演繹については、私は私の権利を主張することが出来る。ここにはこれらの点をいちいち挙げない。有能な読者はこれらの点をよく認め得るであろう。私としては、ジェヴォンス氏の著書と私の著書とは互に他を妨げないで、かえって互に補充し合い、不思議にも互に他の価値を増加し合うものであるといえば足りるのである。これは動かすべからざる私の確信である。私は、これを証明するために、イギリスの
第一版の第二分冊は一八七七年に出版せられた。私はこの中で生産的用役の価格(賃銀、地代、利子)の決定の理論と純収入の率の決定の理論とを説いたが、これらはジェヴォンスのそれとは著しく異っている(四)。
一八七九年に、当時ロンドン大学教授であったジェヴォンスは「経済学の理論」の第二版を公にし、この第二版の序文中で(Pp. XXXV-XLII)、数理経済学の建設の先駆性を一部分ドイツ人ゴッセンに認めている。私がこの先駆性をジェヴォンスに認めたことは、既に読者が知る如くである。ゴッセンについて私は、一八八五年四月及び五月の Journal des
 conomistes に、「忘れられた経済学者ヘルマン・ハインリッヒ・ゴッセン」と題する一文を公にした。その中で私は、ゴッセンの生涯と著書についての解説を与え、併せて、二人の先駆者の著作があるにもかかわらず、新理論のうち結局私自身のものとして残されるべき部分を定めようと努力した(五)。この点を、本書の第十六章の末尾の一節で、再び明らかにするであろう。その所で読者は知られるであろうように、交換において稀少性を考えることのいかに重要であるかは、一八七二年に私共三人とは独立に、ウィーン大学の経済学教授カール・メンガーによってもまた認められ、立証せられているのである。
conomistes に、「忘れられた経済学者ヘルマン・ハインリッヒ・ゴッセン」と題する一文を公にした。その中で私は、ゴッセンの生涯と著書についての解説を与え、併せて、二人の先駆者の著作があるにもかかわらず、新理論のうち結局私自身のものとして残されるべき部分を定めようと努力した(五)。この点を、本書の第十六章の末尾の一節で、再び明らかにするであろう。その所で読者は知られるであろうように、交換において稀少性を考えることのいかに重要であるかは、一八七二年に私共三人とは独立に、ウィーン大学の経済学教授カール・メンガーによってもまた認められ、立証せられているのである。私は、ゴッセンが利用曲線についての先駆者であるのを認め、またジェヴォンスが交換における最大利用の方程式についての先駆者であるのを認める。だが私はこれらの思想を借用したのではない。私は私の経済学説の根本原理を父オーギュスト・ワルラス(Auguste Walras)から借用し、この学説の解説のために函数計算を用いる根本原理をクールノーから借用したのである。これらのことを私は最初の論文で明言し、またそれ以後のあらゆる機会に明言している。今ここでは、この学説が本書の各版で順次にいかに正確さを加えられ、展開せられ、補充せられたかを説明しようと思う。
私は交換方程式、生産方程式、資本化及び信用方程式の解法に、その全体についてはほぼ元のままとしながら、いくつかの細かい部分について修正を加えた。
交換に関しては諸商品の最大利用の定理(六)の基礎的証明のほかに、次の二つの証明を加えた。
(一)利用曲線が連続な場合につき、微分学の通常の記号法による証明||この証明は後に新資本の最大利用の定理を証明するに必要である。(二)利用曲線が不連続な場合の証明。
生産に関しては、均衡の成立のための予備的摸索を仮定し、かつこの運動は有効になされるのではなく、取引証書によって(sur bons)なされると仮定した。そして私はこの仮定をそれ以後においても維持した。
資本化については、交換方程式と最大満足の方程式とから、貯蓄の函数を理論的に演繹し、これを経験的に導き出すことを避けた。そして、純収入率の均等もまた新資本から得られる利用の最大の条件であることを、新定理として証明した。第一版を公にときには、私は新資本用役の最大利用に関する二つの問題のただ一つしか認めることが出来なかった。詳言すれば、ある個人がその収入を種々の欲望の間に配分するに当り資本の量をその当然の性質によって与えられていると考えまたは偶然に決定せられていると想像するときに起る問題、すなわち私が諸商品の最大利用の問題と呼び、数学的には資本用役の稀少性がその価格に比例せねばならぬことによって解かれる問題しか、第一版では私は考えていなかった。しかるに第二版を準備していたとき、なお一つの問題があるのを認めた。それは、社会がその収入の消費に対する超過部分を種々に配分して種々に資本化するに当り、新資本用役の有効利用の最大を目的として、この資本の量を決定しようとするときに現われる問題、すなわち、私が新資本の最大利用の問題と呼び、数学的には資本の稀少性がこの資本の価格に比例せねばならぬことによって解かれる問題である。だから用役の価格と資本の価格とが比例することにより二つの最大が生ずるのであるが、この用役の価格と資本の価格とが比例することは、一の留保の下に、まさしく自由競争によって生ずる結果なのである。
しかしながら、一八七六年以後一八九九年に至る私の研究によって著しく変化せられたのは特に貨幣理論である(七)。第一並びに第二版においては、貨幣編は純理論と応用論との二部から成っていたが、第三、第四版においては、応用論が除かれ、従って純理論、特に貨幣理論の根本である貨幣価値の問題の解法しか研究しなかった。第一版ではこの解法は、私が一般の経済学者から借りてきた「流通に役立った現金」(circulation
 desservir)の思想を基礎としている。第二版においてはこの解法は、拙著(Th
desservir)の思想を基礎としている。第二版においてはこの解法は、拙著(Th orie de la monnaie)に用いられた「所望の現金」(encaisse d
orie de la monnaie)に用いられた「所望の現金」(encaisse d sir
sir e)(訳者註)の思想を基礎としている。だがこの第二版においても第三版においても、第一版におけるように、別に私は貨幣の需要供給の均等方程式を経験的に立てた。この第四版ではそれは、流動資本の需要供給の均等方程式と共に、交換方程式及び最大満足の方程式から理論的に演繹せられている。このようにして流通及び貨幣の理論は、交換の理論、生産の理論、資本化の理論、信用の理論のように、それに相応するシステムの方程式の定立と解法とを含むのである。そしてこの流通論を組成する六章は、純粋経済学の大きな問題の第四である所の流通の問題の解法を示したものである。
e)(訳者註)の思想を基礎としている。だがこの第二版においても第三版においても、第一版におけるように、別に私は貨幣の需要供給の均等方程式を経験的に立てた。この第四版ではそれは、流動資本の需要供給の均等方程式と共に、交換方程式及び最大満足の方程式から理論的に演繹せられている。このようにして流通及び貨幣の理論は、交換の理論、生産の理論、資本化の理論、信用の理論のように、それに相応するシステムの方程式の定立と解法とを含むのである。そしてこの流通論を組成する六章は、純粋経済学の大きな問題の第四である所の流通の問題の解法を示したものである。私は、これら四つの問題の関連を明らかにするため、章編の数、順序、表題に少しく変更を加えた。ことに流通理論を資本化の理論の直後に置き、その次に一編を設け、経済的進歩の研究及び純粋経済学のシステムの研究をこの中に入れた。また限界生産力説すなわち問題の所与としてではなく未知数と考えられた製造係数の決定理論をも、この編の中に加えた。
これらの変化の結果として、本書の概要は次の如くなった。
純粋経済学要論すなわち社会的富の理論
第一編 経済学及び社会経済学の対象と分け方||第二編 二商品相互の間の交換の理論||第三編 多数の商品相互の間の交換の理論||第四編 生産の理論||第五編 資本化及び信用の理論||第六編 流通及び貨幣の理論||第七編 経済的進歩の条件と結果、純粋経済学のシステムの批評||第八編 公定価格・独占・租税について
附録第一 価格決定の幾何学的理論
附録第二 アウスピッツ氏とリーベン氏の価格理論の原理についての考察
この版はかく変化せられてはいるけれども、先にいったように一八七四年|一八七七年のものの最終版に過ぎない。かくいう意味は、私の今の学説が、数学者にして同時に経済学者であった少数の人々が解してくれたような私の第一編 経済学及び社会経済学の対象と分け方||第二編 二商品相互の間の交換の理論||第三編 多数の商品相互の間の交換の理論||第四編 生産の理論||第五編 資本化及び信用の理論||第六編 流通及び貨幣の理論||第七編 経済的進歩の条件と結果、純粋経済学のシステムの批評||第八編 公定価格・独占・租税について
附録第一 価格決定の幾何学的理論
附録第二 アウスピッツ氏とリーベン氏の価格理論の原理についての考察
純粋経済学は、本質的には、絶対的自由競争を仮定した制度の下における価格決定の理論である(八)。稀少であるために、すなわち利用があると共に限られた量しかないために、価格をもつことの出来る有形無形の一切の物の総体は、社会的富を構成する。純粋経済学がまた社会的富の理論であるゆえんはここにある。
社会的富を組成する物のうちに、一回以上役立つ物すなわち資本または持続財と、一回しか役立たない物すなわち収入または消耗財(biens fongibles)とを区別せねばならぬ。資本は土地、人的能力及び狭義の資本を含む。収入は第一に消費の目的物及び原料を含む。これらは多くの場合有形の物である。次に収入はいわゆる用役(services)すなわち資本の継続的使用を含む。これらの用役は多くの場合無形のものである。資本の用役で直接的利用を有するものは、消費的用役(services consommables)と称せられ、消費目的物に結合する。間接的利用しかもたない資本の用役は、生産的用役(services producteurs)と称せられ、原料と結合する。私は、ここにこそ純粋経済学全体の鍵があると思う。もし資本と収入との区別を看過し、あるいはことに、社会的富のうちに有形の収入と
まず消費目的物と消費的用役とのみが売買せられる市場、換言すればそれらのもののみが交換せられる市場を想像し、かつそこでは用役の販売が資本の賃貸によって行われると想像する。これらのもののうちから価値尺度財として採択せられた物で表わしたこれらの物または用役の価格すなわち交換比率が偶然に叫ばれると、各交換者は、自らある一定期間の消費に比較的に過剰に所有していると信ずる物または用役を、これらの価格で供給し、自ら不充分であると信ずる物または用役を需要する。かくの如くにして各商品の有効に需要せられる量と供給せられる量は決定されるのであるが、需要が供給を超える物の価格は騰貴せしめられ、供給が需要を超える物の価格は下落せしめられる。このようにして叫ばれた新しい価格に対して、各交換者は
次に交換の問題の中に、消費の目的物が生産的用役の相互の結合によって生ずる所のまたは生産的用役を原料に適用することによって生ずる所の生産物であるという事情を導き入れて、我々は生産の問題を提出する。この事情を考慮に入れるには、用役の売手であると同時に消費的用役及び消費の目的物の買手である地主、労働者、資本家の面前に、生産物の売手としてのまた生産的用役及び原料の買手としての企業者を置かねばならぬ。この企業者の目的は、生産的用役を生産物に変化して利益を得るにある。生産物は、彼ら企業者が相互に売買し合う原料であることもあれば、彼ら企業者に生産的用役を売った地主、労働者、資本家に販売せられる消費の目的物であることもある。だがこれらの現象をよく了解するためには、一つの市場の代りに、用役の市場([#「(」は底本では欠落]march
 des services)と生産物の市場(march
des services)と生産物の市場(march des produits)とを想像するがよい。用役の市場ではこれらの用役は地主、労働者、資本家のみによって供給せられ、消費的用役は地主、労働者、資本家によって需要せられ、生産的用役は企業者によって需要せられる。生産物の市場では生産物は企業者のみによって供給せられ、原料はこの同じ企業者によって需要せられ、消費の目的物は地主、労働者、資本家によって需要せられる。これら二つの市場においては、偶然に叫ばれた価格で、地主、労働者、資本家であって同時に消費者である者が用役を供給し、消費的用役と消費の目的物とを需要し、それにより、考えられた期間中に出来るだけ多くの利用を得ようとし、生産者である企業者は生産物を供給し、また生産的用役で表わした製造係数の割合に従って同じ期間中に処分すべき生産的用役または原料を需要する。そしてこれらの生産者である企業者は、生産物の販売価格が生産的用役から成る生産費に超過する場合には生産を拡張し、反対に生産的用役から成る生産費が生産物の販売価格を超えるときは生産を縮小する。各市場では人々は、需要が供給を超えるときは、価格を騰貴せしめ、供給が需要を超過するときは、これを下落せしめる。均衡市場価格は、各用役または生産物の需要と供給とを等しからしめる価格であり、また各生産物の販売価格を生産的用役から成る生産費に等しからしめる価格である。
des produits)とを想像するがよい。用役の市場ではこれらの用役は地主、労働者、資本家のみによって供給せられ、消費的用役は地主、労働者、資本家によって需要せられ、生産的用役は企業者によって需要せられる。生産物の市場では生産物は企業者のみによって供給せられ、原料はこの同じ企業者によって需要せられ、消費の目的物は地主、労働者、資本家によって需要せられる。これら二つの市場においては、偶然に叫ばれた価格で、地主、労働者、資本家であって同時に消費者である者が用役を供給し、消費的用役と消費の目的物とを需要し、それにより、考えられた期間中に出来るだけ多くの利用を得ようとし、生産者である企業者は生産物を供給し、また生産的用役で表わした製造係数の割合に従って同じ期間中に処分すべき生産的用役または原料を需要する。そしてこれらの生産者である企業者は、生産物の販売価格が生産的用役から成る生産費に超過する場合には生産を拡張し、反対に生産的用役から成る生産費が生産物の販売価格を超えるときは生産を縮小する。各市場では人々は、需要が供給を超えるときは、価格を騰貴せしめ、供給が需要を超過するときは、これを下落せしめる。均衡市場価格は、各用役または生産物の需要と供給とを等しからしめる価格であり、また各生産物の販売価格を生産的用役から成る生産費に等しからしめる価格である。資本化の問題を解くには、貯蓄をする地主、労働者、資本家すなわち自ら供給する用役の価値の全部をあげて消費的用役及び消費目的物を需要することなく、この価値の一部をもって新資本を需要する換言すれば貯蓄する地主、労働者、資本家の存在を仮定せねばならない。そしてこれら貯蓄創造者に相対して、原料または消費の目的物を製造することなく新資本を製造する企業者の存在を仮定せねばならぬ。一方においてはある額の貯蓄と他方においてはある額の新資本とを与えられたとすれば、これらの貯蓄と新資本とは新資本の市場において、せり上げせり下げの機構に従い、交換理論と生産理論とによって決定せられた、新資本の消費的用役または生産的用役の価格に応じて互に交換せられる。そこで収入のある一定の率が成立し、各新資本の販売価格はその用役の価格と収入の率の比に等しくなる。新資本の企業者は、生産物の企業者と同じく、販売価格が生産費を超えるかまたは生産費が販売価格を超えるかに従い、その生産をあるいは拡張し、あるいは縮小する。
一度収入の率が得られると、ただに新固定資本の価格のみでなく、また旧固定資本すなわち既に存在する土地、人的能力、狭義の資本の価格が得られる。これは旧資本の用役の価格である地代、賃銀、利子をこの率で除すことによって得られる。残るのは流動資本の価格を見出すことと、価値尺度財が貨幣である場合にこれらすべての価格がいかなるものとなるかを知ることとだけである。これらは流通及び貨幣の問題である。
読者はこの第四版において私が「所望の現金」の考察により、いかにして静学的観点を離れることなく、先の問題を取扱ったと同じ条件と方法とをもって、右の問題を提出し、解決することが出来たかを見ることが出来よう。この問題の提出と解決のためには、流動資本を物または貨幣の形態をとる所の予備(approvisionnement)の用役を果すものと考え、かつこれらの用役を、資本家によってのみ供給せられ、地主、労働者、資本家によっては消費的用役として需要せられ、企業者によっては、予備の用役で表わした製造係数の割合に従って、生産的用役として需要せられると考えれば足る。かくてこれら予備の用役の市場価格は狭義の用役の市場価格の如くにして決定せられる。そして流動資本及び貨幣の価格もまた予備の用役の価格の純収入率に対する比として生ずるのであって、貨幣の価格は、貨幣が貨幣である限り、その量の反比例函数として成立する。
ところでこの全理論は数学的理論である。語を換えていえばその説明が通常の語でなされ得るとしても、その証明は数学的になされねばならぬ。それは全く交換理論の基礎の上に立つのであり、交換理論はすべて市場の均衡状態における二つの事実に約言される。まず交換者が利用の最大を得る事実、次にすべての交換者が需要する各商品の量と供給する量とは相等しいとの事実に要約される。ところでひとり数学によってのみ我々は利用の最大の条件を知ることが出来るのである。我々は数学によって、各交換者につき、各消費の目的物または消費的用役に対し、それらの
右のようなシステムについて、本書において出来る限り入念で詳細な説明を与えようと思う。しかし私はこれを既に一八七三年から一八七六年に亙って「社会的富の数学的理論」(Th
 orie math
orie math matique de la richesse sociale)の初めの四章に解説し、また一八七四年と一八七七年とに純粋経済学理論の第一版に解説し、証明した。私はこの全理論の原理を得るや否や、これをパリーの精神科学及び政治学学士院に報告するのを私の義務と感じた。そこで右に挙げた四論文の第一を
matique de la richesse sociale)の初めの四章に解説し、また一八七四年と一八七七年とに純粋経済学理論の第一版に解説し、証明した。私はこの全理論の原理を得るや否や、これをパリーの精神科学及び政治学学士院に報告するのを私の義務と感じた。そこで右に挙げた四論文の第一を事情に通暁したすべての人々がよく知るように、価格は充された最後の欲望の強度すなわち Final Degree of Utility あるいは Grenznutzen に比例するとの学説、ジェヴォンスとメンガー氏と私とがほとんど時を同じゅうして考え出した理論、全経済学の基礎を作ったこの理論は、イギリス、オーストリア、アメリカ、そのほか純粋経済学が研究せられ教授せられる諸国において、経済学上の定説となった。
ところで交換理論の原理が経済学に入ってから、生産理論の原理もまたまもなく経済学に入ってこざるを得なかったが、事実において入ってきた。ジェヴォンスは「経済学の理論」の第二版において、第一版に認めなかったものを認めた。それは、利用の最終度が生産物の価格を決定する瞬間から、これがまた生産的用役の価格すなわち地代、賃銀、利子を決定するというにある。なぜなら自由競争の制度の下においては、生産物の販売価格は生産的用役から成る生産費に等しくなるからである。ジェヴォンスは、彼の著書の第二版の序文の終りのはなはだ興味深い十頁(Pp. XLIII-LVII)において、イギリス派の方式または少くともリカルド・ミル派の方式を全く変えて、生産的用役の価格により生産物の価格を決定する代りに、生産物の価格により生産的用役の価格を決定せねばならぬと明言している。この大きな発展の可能である指示はイギリスでは直ちに追随はされなかった。かえってジェヴォンスの思想に対する反動が起って、リカルドの生産費理論が有力となった。しかるに自ら限界利用の概念を把握したオーストリアの経済学もまた、この結果を論理的に生産理論のうちに押しつめて、生産物の価値と生産手段の価値との間に、私が生産物の価値と原料及び生産的用役の価値との間に導き入れた関係と全く同じ関係を導き入れたのである。
けれども我々の一致は、資本化の理論に関してはそれほど完全ではない。この問題についてメンガー氏は Jahrb
 cher f
cher f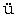 r National
r National konomie und Statistik, tome XVII 中に彼の研究「資本理論について」(Zur Theorie des Kapitals)を公にし、またインスブルック(Innsbruck)の教授ベェーム=バウェルク氏はその著書「資本と利子」(Kapital und Kapitalzins)(一八八四年、一八八九年)を完成した。ベェーム=バウェルク氏はこの書物の中で、資本利子の事実を現在財の価値と将来財の価値との差から引き出した(九)。私は、ここではベェーム=バウェルク氏と意見を同じゅうしないことを言明せねばならぬし、かつ
konomie und Statistik, tome XVII 中に彼の研究「資本理論について」(Zur Theorie des Kapitals)を公にし、またインスブルック(Innsbruck)の教授ベェーム=バウェルク氏はその著書「資本と利子」(Kapital und Kapitalzins)(一八八四年、一八八九年)を完成した。ベェーム=バウェルク氏はこの書物の中で、資本利子の事実を現在財の価値と将来財の価値との差から引き出した(九)。私は、ここではベェーム=バウェルク氏と意見を同じゅうしないことを言明せねばならぬし、かつ「n年の後にしか引渡されないでAなる価値をもつべき物を想像し、この物が今直ちに引渡されるとすると、利子の年率がiであるとき、それは現在


数学者はそれを判断するであろう。しかし既に今から私の立場を示しておいてもよいものがある。ジェヴォンスの理論と私の理論とは、現われるとまもなくヒューウェル(Whewell)及びクールノーの古い試みと共にイタリア語に訳出された。またドイツでは、初め忘れられながらもゴッセンの著作が、既に知られていたチューネンやマンゴルトらの著作に加えられた。その後またドイツ、オーストリア、イギリス、イタリア、アメリカにおいて、数理経済学の多数の文献が現われた(一一)。このようにして形成せられる学派は、すべてのシステムのうちで、真に科学を構成すべきシステムとして異彩を放つであろう。数学を知らず、数学がいかなるものであるかをさえ正確に知らないで、数学は経済学の原理の解明に役立たぬときめ込んでいる経済学者に至っては、「人間の自由は方程式に表わすことが出来ない」とか、「数学はすべての精神科学に存する摩擦を捨象する」とか、またはこれらと同様の力しか無い他愛もないことを繰り返して去っていくがよかろう。彼らは、自由競争における価格決定の理論が数学的理論にならぬようにと努めている。だから彼らは数学を避けて、純粋経済学の基礎なくして応用経済学を構成していくか、それとも必要な根底もなく純粋経済学を構成して、はなはだ悪い純粋経済学またははなはだ悪い数学を構成するか、これらのいずれか一つを選ばねばならぬ。私は第四十章で私の理論のように数学的理論である所の理論の標本をあげた。これらの理論と私の理論との相異は、私が私の問題における未知数だけの方程式を得ようと努めたのに反し、これらの人々は二つの方程式によって一つの未知数を決定しようとしたり、二つ、三つまたは四個の未知数を決定するのに一つの方程式を用いる点にある。私は、人々が、これらの人々のこのような方法を、純粋経済学を精密科学として構成する方法に全く相反するものとして、疑われることを望む者である。
精密科学としての経済学が遠からず樹立せられるであろうか、または遠い将来においてしか樹立せられるに至らないであろうか。それらは私の問題ではなく、ここに論ずるを要しない。今日ではたしかに経済学は天文学の如く、力学の如く、経験的であり同時に合理的な科学である。我々は経済学の経験的性質でこの合理的性質を
ローザンヌ、一九〇〇年六月
レオン・ワルラス
註一 この書の印刷用の紙型が出来上ってから、第三七六頁と第四一四頁とにわずかの修正を加え、かつ一九〇二年日付の二つの註を添えた。(一九〇二年記す)
註二 これら第二、第三部に代えて、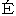 tudes d'
tudes d' conomie sociale(1896)と
conomie sociale(1896)と 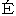 tudes d'
tudes d' conomie appliqu
conomie appliqu e(1898)との二巻を公にした。これで私の仕事はほぼ完成したわけである。
e(1898)との二巻を公にした。これで私の仕事はほぼ完成したわけである。
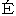 tudes d'
tudes d' conomie sociale(1896)と
conomie sociale(1896)と 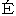 tudes d'
tudes d' conomie appliqu
conomie appliqu e(1898)との二巻を公にした。これで私の仕事はほぼ完成したわけである。
e(1898)との二巻を公にした。これで私の仕事はほぼ完成したわけである。註三 Compte-rendu des s ances et travaux de l'Acad
ances et travaux de l'Acad mie des sciences morales et politiques, janvier 1874. または Journal des
mie des sciences morales et politiques, janvier 1874. または Journal des  conomistes, avril et juin 1874. 参照。
conomistes, avril et juin 1874. 参照。
 ances et travaux de l'Acad
ances et travaux de l'Acad mie des sciences morales et politiques, janvier 1874. または Journal des
mie des sciences morales et politiques, janvier 1874. または Journal des  conomistes, avril et juin 1874. 参照。
conomistes, avril et juin 1874. 参照。註四 純粋経済学要論の第一版の第一分冊は、Principe d'une th orie math
orie math matique de l'
matique de l' change 及び Equation de l'
change 及び Equation de l' change と題せられる二箇の論文に要約せられ、一は一八七三年パリの Acad
change と題せられる二箇の論文に要約せられ、一は一八七三年パリの Acad mie des sciences morales et politiques に、他は一八七五年十二月ローザンヌの Soci
mie des sciences morales et politiques に、他は一八七五年十二月ローザンヌの Soci t
t vaudoise des sciences naturelles に報告せられた。第二分冊は Equation de la production 及び Equation de la capitalisation et du cr
vaudoise des sciences naturelles に報告せられた。第二分冊は Equation de la production 及び Equation de la capitalisation et du cr dit と題する二論文に要約せられ、出版前に、一は一八七六年一月と二月、他は七月 Soci
dit と題する二論文に要約せられ、出版前に、一は一八七六年一月と二月、他は七月 Soci t
t vaudoise に報告せられた。これら四箇の論文は Teoria matematica della richezza sociale(Biblioteca dell'economista. 1878.)という書名の下にイタリー語に訳され、また Mathematische Theorie der Preisbestimmung der wirtschaftlichen G
vaudoise に報告せられた。これら四箇の論文は Teoria matematica della richezza sociale(Biblioteca dell'economista. 1878.)という書名の下にイタリー語に訳され、また Mathematische Theorie der Preisbestimmung der wirtschaftlichen G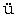 ter(Stuttgart. Verlag von Ferdinand Enke. 1881)という書名の下にドイツ語に訳出された。(邦訳、早川三代治訳レオン・ワルラアス純粋経済学入門。)
ter(Stuttgart. Verlag von Ferdinand Enke. 1881)という書名の下にドイツ語に訳出された。(邦訳、早川三代治訳レオン・ワルラアス純粋経済学入門。)
 orie math
orie math matique de l'
matique de l' change 及び Equation de l'
change 及び Equation de l' change と題せられる二箇の論文に要約せられ、一は一八七三年パリの Acad
change と題せられる二箇の論文に要約せられ、一は一八七三年パリの Acad mie des sciences morales et politiques に、他は一八七五年十二月ローザンヌの Soci
mie des sciences morales et politiques に、他は一八七五年十二月ローザンヌの Soci t
t vaudoise des sciences naturelles に報告せられた。第二分冊は Equation de la production 及び Equation de la capitalisation et du cr
vaudoise des sciences naturelles に報告せられた。第二分冊は Equation de la production 及び Equation de la capitalisation et du cr dit と題する二論文に要約せられ、出版前に、一は一八七六年一月と二月、他は七月 Soci
dit と題する二論文に要約せられ、出版前に、一は一八七六年一月と二月、他は七月 Soci t
t vaudoise に報告せられた。これら四箇の論文は Teoria matematica della richezza sociale(Biblioteca dell'economista. 1878.)という書名の下にイタリー語に訳され、また Mathematische Theorie der Preisbestimmung der wirtschaftlichen G
vaudoise に報告せられた。これら四箇の論文は Teoria matematica della richezza sociale(Biblioteca dell'economista. 1878.)という書名の下にイタリー語に訳され、また Mathematische Theorie der Preisbestimmung der wirtschaftlichen G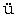 ter(Stuttgart. Verlag von Ferdinand Enke. 1881)という書名の下にドイツ語に訳出された。(邦訳、早川三代治訳レオン・ワルラアス純粋経済学入門。)
ter(Stuttgart. Verlag von Ferdinand Enke. 1881)という書名の下にドイツ語に訳出された。(邦訳、早川三代治訳レオン・ワルラアス純粋経済学入門。)註五 この論文は 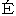 tudes d'
tudes d' conomie sociale 中に収められている。
conomie sociale 中に収められている。
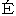 tudes d'
tudes d' conomie sociale 中に収められている。
conomie sociale 中に収められている。註六 私は maxima(複数)といって、maximum(単数)といわない。Th orie de la monnaie の初めの二編を、La Revue scientifique の一八八六年四月号に公にしたとき、この雑誌の校正係であるパリ人は、ラテン語の形容詞 maximum を名詞に一致せしめるべきものと考え、これを訂正した。私はこの校正係の処置は普通の用法に一致するものと考え、それを採用することにした。
orie de la monnaie の初めの二編を、La Revue scientifique の一八八六年四月号に公にしたとき、この雑誌の校正係であるパリ人は、ラテン語の形容詞 maximum を名詞に一致せしめるべきものと考え、これを訂正した。私はこの校正係の処置は普通の用法に一致するものと考え、それを採用することにした。
 orie de la monnaie の初めの二編を、La Revue scientifique の一八八六年四月号に公にしたとき、この雑誌の校正係であるパリ人は、ラテン語の形容詞 maximum を名詞に一致せしめるべきものと考え、これを訂正した。私はこの校正係の処置は普通の用法に一致するものと考え、それを採用することにした。
orie de la monnaie の初めの二編を、La Revue scientifique の一八八六年四月号に公にしたとき、この雑誌の校正係であるパリ人は、ラテン語の形容詞 maximum を名詞に一致せしめるべきものと考え、これを訂正した。私はこの校正係の処置は普通の用法に一致するものと考え、それを採用することにした。註七 これらの研究のうち、Notes sur le 15 1/2 l gal; Th
gal; Th orie math
orie math matique du bim
matique du bim tallisme; De la fixit
tallisme; De la fixit de valeur de l'
de valeur de l' talon mon
talon mon taire(Journal des
taire(Journal des  conomistes. 一八七六年十二月、一八八一年五月、一八八二年十月所載);
conomistes. 一八七六年十二月、一八八一年五月、一八八二年十月所載); 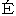 quations de la circulation(Bulletin de la Soci
quations de la circulation(Bulletin de la Soci t
t vaudoise des sciences naturelles. 一八九九年所載)は純理論の研究であって、これらは本書中に収められている。D'une m
vaudoise des sciences naturelles. 一八九九年所載)は純理論の研究であって、これらは本書中に収められている。D'une m thode de r
thode de r gularisation de la variation de valeur de la monnaie(一八八五年); Th
gularisation de la variation de valeur de la monnaie(一八八五年); Th orie de la monnaie(一八八六年); Le probl
orie de la monnaie(一八八六年); Le probl me mon
me mon taire(一八八七年|一八九五年)は応用論の研究であって、これらは
taire(一八八七年|一八九五年)は応用論の研究であって、これらは 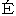 tudes d'
tudes d' conomie politique appliqu
conomie politique appliqu e 中に収められている。
e 中に収められている。
 gal; Th
gal; Th orie math
orie math matique du bim
matique du bim tallisme; De la fixit
tallisme; De la fixit de valeur de l'
de valeur de l' talon mon
talon mon taire(Journal des
taire(Journal des  conomistes. 一八七六年十二月、一八八一年五月、一八八二年十月所載);
conomistes. 一八七六年十二月、一八八一年五月、一八八二年十月所載); 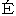 quations de la circulation(Bulletin de la Soci
quations de la circulation(Bulletin de la Soci t
t vaudoise des sciences naturelles. 一八九九年所載)は純理論の研究であって、これらは本書中に収められている。D'une m
vaudoise des sciences naturelles. 一八九九年所載)は純理論の研究であって、これらは本書中に収められている。D'une m thode de r
thode de r gularisation de la variation de valeur de la monnaie(一八八五年); Th
gularisation de la variation de valeur de la monnaie(一八八五年); Th orie de la monnaie(一八八六年); Le probl
orie de la monnaie(一八八六年); Le probl me mon
me mon taire(一八八七年|一八九五年)は応用論の研究であって、これらは
taire(一八八七年|一八九五年)は応用論の研究であって、これらは 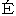 tudes d'
tudes d' conomie politique appliqu
conomie politique appliqu e 中に収められている。
e 中に収められている。(訳者註) "encaisse d sir
sir e" はケインズの交換方程式におけるkと等しい意味をもっている。
e" はケインズの交換方程式におけるkと等しい意味をもっている。
 sir
sir e" はケインズの交換方程式におけるkと等しい意味をもっている。
e" はケインズの交換方程式におけるkと等しい意味をもっている。註八 ここで自由競争の制度というのは、用役をせり下げつつ売る者及び生産物をせり上げつつ買う者の自由競争の制度を意味する。企業者の自由競争の場合には、一八八節に説明するように、これのみが価値を生産費の高さに一致せしめる唯一の方法ではない。また応用経済学は、この制度が常に最良の制度であるか否かを問わねばならない。
註九 メンガーの論文とベェーム=バウェルク氏の著書とは、Revue d' conomie politique(一八八八年十一、十二月、一八八九年、三、四月)によく分析されている。
conomie politique(一八八八年十一、十二月、一八八九年、三、四月)によく分析されている。
 conomie politique(一八八八年十一、十二月、一八八九年、三、四月)によく分析されている。
conomie politique(一八八八年十一、十二月、一八八九年、三、四月)によく分析されている。註一〇 次の一節は本書第二版(一八八九年五月)の序文の一節そのままである。たとい私が、私の著書のうちでは、貯蓄の函数を経験的に導き出していても、既にこの序文のうちで、あるいは純収入率の増加函数としてあるいはその減少函数として、演繹的にこれを導き出す方法を示しているのを、読者は知られるであろう。
註一一 これら数理経済学の文献は、古い数理経済学文献と共に、M. T. N. Bacon が英訳したクールノーの訳書の巻末に I. Fisher が載せた数理経済学文献中に詳 かである。この訳書は Economic Classics 中の一冊として一八九七年に公にされた。
[#改丁]第一編 経済学及び社会経済学の目的と分け方
[#改丁]
第一章 スミスの定義とセイの定義
要目 一 定義の必要。二 フィジオクラシー。三 スミスによって経済学に課せられた二つの目的。(一)人民に収入すなわち豊富な生活を得せしめること。(二)国家に充分な収入を与えること。四 第一の観察。二つの目的は等しく重要であるが、いずれも本来の科学の目的ではない。経済学については別の見解がある。五 第二の観察。二つの活動は等しく重要であるが、異る性質をもっている。前者は利益、後者は公正。六 セイが考察した経済学は富が形成せられ、分配せられ、消費せられる方法の単なる記述である。七 自然主義者の見解は社会主義の排撃を容易ならしめるが部分的に不正確である。富の生産または分配については人は最も有用なまたは最も公正な組合せを選ばねばならぬ。八 経験的な分け方。九 ブランキ及びガルニエの不完全な訂正。
一 経済学の講義または概論の当初にまず、経済学それ自身、その目的、その分け方、その性格、その限界を限定せねばならない。私はこの義務を回避しようとは思わない。だが断っておかねばならぬが、この義務は、人々がおそらく想像するであろう以上に、果すに困難であり、簡単ではない。経済学の正しい定義は未だにないのである。既に経済学に与えられたすべての定義のうちで、科学上に獲得された真理の象徴である所の一般的で決定的な承認を得ているものは、一つとして無い。私はそれらのうち比較的に最も興味あるものを引用し批評し、しかる後私の定義を示すに努めたいと思う。そしてこれらのことをなす間に、我々が知っておかねばならぬ若干の著者名や著作名や時日等を挙げる機会を作るであろう。
二 最初の重要な経済学者の集団はケネーとその弟子達である。彼らは共通の学説をもち、一つの学派を作った。彼らは自らこの学説をフィジオクラシー(社会の自然的統治を意味する)と呼んだ。今日彼らをフィジオクラットと呼ぶのは、この理由に
 t
t s politiques, 1767)の著者メルシエ・ド・ラ・リヴィエール(Mercier de la Rivi
s politiques, 1767)の著者メルシエ・ド・ラ・リヴィエール(Mercier de la Rivi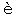 re)、「フィジオクラシーまたは人類に最も有利な統治の自然的構成」(Physiocratie ou constitution naturelle du gouvernement le plus avantageux au genre humain, 1767, 1768)、著者デュポン・デュ・ヌムール(Dupont du Nemours)、ボードー僧正(L'Abb
re)、「フィジオクラシーまたは人類に最も有利な統治の自然的構成」(Physiocratie ou constitution naturelle du gouvernement le plus avantageux au genre humain, 1767, 1768)、著者デュポン・デュ・ヌムール(Dupont du Nemours)、ボードー僧正(L'Abb Baudeau)、ル・トローヌ(Le Trosne)である。チュルゴーはこの派の人ではない。フィジオクラットは、彼らの著作の書名で
Baudeau)、ル・トローヌ(Le Trosne)である。チュルゴーはこの派の人ではない。フィジオクラットは、彼らの著作の書名で三 アダム・スミスは、一七七六年に公にした国富論において、初めて経済学の材料を結合して統一体となすのに成功した。ところでスミスが経済学の定義を与えようとしているのは、「経済学の体系について」と題する第四編の序説の当初においてである。そこで彼が下している定義は次の如くである。「経済学、立法者または政治家の知識の一分枝として考えられる経済学は二つの異った目的をもっている。その一つは人民に豊富な収入すなわち豊富な生活を得せしめること、より適切な言葉でいえば、人民をして自ら豊富な収入すなわち豊富な生活を得ることの出来る地位に置くことにある。他の一つは国家または公共団体に公務に必要な収入を得せしめることにある。一言にいえば、経済学は人民と主権者とを富ますことを目的とする。」この定義は経済学の父と呼ばれる人によって下されたものではあり、かつまた彼の著作の当初に掲げられたものではなくて、自ら問題の内容を充分に知り得た後に、その中央部に取扱われたものであるから、我々の充分な研究に値する。それには考慮せられるべき二つの点が含まれていると思う。
四 人民に豊富な収入を得せしめ、国家に充分な収入を得せしめること、それらはたしかにはなはだ重要な二つの目的である。そして経済学がこれらの目的を達せしめるとすれば、経済学は著しく我々の役に立つわけである。けれども私はいわゆる科学の目的がそこにあるとは思わない。実際本来の科学の特質は有益なまたは有害な結果に無関心に、純粋の真理を追求していく所にある。だから幾何学が二等辺三角形は二等角三角形であるとの命題を立言するとき、また天文学が遊星は太陽が中心をなしている楕円の軌道をめぐるとの命題を立言するとき、これら幾何学や天文学は本来の科学である。これら二つの真理の第一が他の幾何学上の真理と同じく建築の骨組に、石材の切り方に、家屋の建設に、貴い結果を
五 スミスの定義についての右の考察は、科学の目的に関するものである。私はその性質についても同様に重大な考察をしておかねばならぬ。
人民に豊富な収入を得せしめかつ国家に充分な収入を得せしめることは、共に重要にして微妙な活動ではあるが、しかし全く異る性質の活動である。前者は農業工業商業を一定の状態に置こうとすることから成立つ。これらの状態が有利なものであるかまたは不利であるかに従い、農業・商業・工業の生産はあるいは豊富となり、あるいは減少する。だから既に知られているように、職人組合、同業組合、親方の制度、厳重な干渉制限の制度、公定価格制度等の下においては、産業は悩み続け、空しく時を過した。今日では労働の自由と交換の自由の制度の下に産業は繁栄している。条件は前の場合には有利であり、後の場合には不利である。だが二つの場合ともに不利となりまたは有利となったものは、個人の利益のみである。冒されたものまたは尊重せられたものは正義ではない。国家に充分な収入を得せしめようとする場合は、これと異る。そこには国家の収入を構成するに必要なものを、個人の収入から徴収する活動がある。これは、よい条件で行われることもあれば、悪い条件でなされることもある。そしてこれらの条件がよいかまたは悪いかによって、国家の収入が充分となりまたは不充分となるのみでなく、また個人が公正に取扱われるかまたは不公正に取扱われるかの結果が生じてくる。すなわち各人の負担が公正になされるか、または不公正のためにある者が犠牲に供せられ、他の者が特権を得ているかの結果が起る。このようにして、社会のある階級が租税の負担を免れ、それがある他の階級にのみ課せられたことがあった。それが明白な不正義であることは、今日認められている所である。要するに人民に豊富な収入を得せしめることは有益な仕事をなすことであり、国家に充分な収入を供給することは公正の仕事をなすことである。利用と公正、利益と正義とははなはだしく異る種類の観点である。従ってスミスは例えば経済学の目的はまず第一に社会的収入を豊富ならしめる生産条件を示すにあり、次に作られた生産物を個人と国家との間に分配する条件を示すにあるといって、この区別を明らかにしたらよかったと思う。この定義の方がよりよいであろう。だがこれをもってしてもなお、経済学の真に科学的な部分は依然として明らかにせられていない。
六 歴史的順序からはスミスの後に来るジ・ベ・セイ(Jean-Baptiste Say)は経済学上最も有名な名の一つであるが、彼はスミスの定義について次の如くいう。「経済学は、富が形成せられ、分配せられ、消費せられる道行を知らしめるものだ、と私は言いたい。」彼の著書[#「著書」は底本では「著者」]は一八〇三年に第一版を出し、第二版は執政政府の検閲に基き発売を禁止せられ、第一帝国の転落後にしか公にせられなかったが、それは「経済学概論、または富が形成せられ、分配せられ、消費せられる方法の簡単な解説」(Trait
 d'
d' conomie politique, ou simple exposition de la mani
conomie politique, ou simple exposition de la mani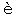 re dont se forment, se distribuent et se consomment les richesses)と題せられている。この定義とこの書物が採った分け方とは、経済学者が一般に承認し、追随しているものである。それはたしかに、人々がクラシックと考えようとしている定義であり、分け方である。だが私は、これに従い得ないと主張するのを許してもらわねばならぬ。そしてその理由は、この定義と分け方とを成功せしめたその点にまさしくあるのである。
re dont se forment, se distribuent et se consomment les richesses)と題せられている。この定義とこの書物が採った分け方とは、経済学者が一般に承認し、追随しているものである。それはたしかに、人々がクラシックと考えようとしている定義であり、分け方である。だが私は、これに従い得ないと主張するのを許してもらわねばならぬ。そしてその理由は、この定義と分け方とを成功せしめたその点にまさしくあるのである。七 一見して明らかであるように、セイの定義はスミスのそれと異るのみでなく、ある意味においてはそれと正反対である。スミスを信ずる限り全経済学は科学であるよりはむしろ技術であり(第四節)、セイに従えばそれは自然科学である。セイによれば、富は全く自然的ではないにしても、少くとも人間の意志とは独立の態様で形成せられ、分配せられ、消費せられるのであり、全経済学はこの態様の単純なる解説であるようである。
セイがこの定義のうちで経済学に与えた自然科学的色彩は、経済学者を
 conomie politique, 2 vol., 1851-3)中の記事、例えばシャール・コックラン(Charles Coquelin)が執筆した競争、経済学、産業、コッシュー(Cochut)が執筆した道徳等を読まねばならぬ。そこには最も意味深い諸句が見出される[#「見出される」は底本では「見出させる」]。
conomie politique, 2 vol., 1851-3)中の記事、例えばシャール・コックラン(Charles Coquelin)が執筆した競争、経済学、産業、コッシュー(Cochut)が執筆した道徳等を読まねばならぬ。そこには最も意味深い諸句が見出される[#「見出される」は底本では「見出させる」]。不幸にしてこの見方ははなはだ便利ではあるが、はなはだしく
八 スミスの定義は不完全であるに過ぎないが、セイの定義はこれに劣り、不正確である。またこの定義から出てくる分け方も全く経験的であると、私は附言しておく。所有権の理論、租税の理論は実はまず孤立して考えられた社会人の間の、次に国家として集団的に考えられた人の間の富の分配の唯一の理論の各半面に過ぎないもので、かつ二つは共に道徳の原理に密接に依存しているのであるが、それらは
九 セイの弟子らのある者は、セイの定義の欠点を知っていたが、あえて修正しなかった。アドルフ・ブランキ(Adolphe Blanqui)はいっている。「ドイツ並びにフランスでは、今日経済学は、一般に考えられている領域を脱出している。ある経済学者は経済学を普遍的科学となそうとし、他の人は狭いかつ通俗的に考えられている範囲に限ろうとする。フランスにおいてこれら両極端の意見の間に存する
ブランキに次いで、ジョセフ・ガルニエ(Joseph Garnier)はいっている。「経済学は自然科学であり、同時に規範科学である。これらの二つの観点から、経済学は、ある所のものと、物の自然的流れに従い正義の観念に一致してあるべき所のものとを証明する。」そこでガルニエはセイの定義に少しく附け加えて、それを修正しようとした。曰く、「経済学は富の科学である」すなわちいかにして富が、個人及び社会の利益となるように、最も合理的に(もちろん正義に合するように)生産せられ、分配せられ、消費せられるか、またはせられるべきかを決定することを目的とする科学である」と。ここでガルニエは彼の学派の軌道から離れようとして、真剣でかつ賞讃すべき努力をなしている。しかし二つの定義を接ぎ合して作った合金が、いかに奇妙で支離滅裂であるかを不思議にも彼は認めなかった。これは、経済学者に哲学がないことの好例であって、明快と正確とを主な特質とするフランス経済学者の精神の美点を打ち消してしまう。経済学はいかにして自然科学であり、同時に規範科学であり得るか。いかにしてかかる科学を考え得るか。一方においていかにして富が最も公正に分配せられねばならぬかを研究の目的とする科学が、他方においていかにして富が最も自然的に生産せられるかを研究の目的とする自然科学となり得るか。またこの自然科学は富を豊富に生産すべき技術にもならねばなるまい。要するにセイの定義もスミスのそれに帰するのであって、経済学の真の自然科学的性質は依然として明らかにせられていない。
私はこれを明らかにしようと思う。必要ならば経済学を自然科学、規範科学、政策に分けよう。そしてそれがため、我々はまずあらかじめ、科学と政策と道徳との区別を明らかにせねばならない。
[#改ページ]
第二章 科学と政策と道徳との区別
要目 一〇 政策は忠告し、命令し、指導する。科学は観察し、記述し、説明する。一一 科学と政策の区別と理論と実際の区別とは全く別である。一二 科学は政策に光を与える。政策は科学を利用する。一三 一つの科学によって与えられる理論は多くの政策に光を与え得る。一つの政策は多くの科学によって与えられる理論を利用することが出来る。一四、一五 区別は優れているが不充分である。一六 科学は事実の研究である。一七 第一の区別。自然力の働きをその起源とする自然的事実。人間の意志の作用にその起源をもつ人間的事実。自然的及び人間的事実は純粋科学(狭義の科学と歴史)の対象である。一八 第二の区別。産業上の人間的事実、すなわち人格と物との関係。道徳上の人間的事実、すなわち人格と人格との関係。一九 産業的事実は応用科学すなわち政策の対象である。道徳的事実は精神科学すなわち道徳学の対象である。二〇 真。利用。善はそれぞれ科学、政策、道徳の規準である。
一〇 既に幾年かを経過していることであるが、好著「信用及び銀行概論」(Trait
 du cr
du cr dit et des banques)の著者でまた「経済学辞典」(Dictionnaire d'
dit et des banques)の著者でまた「経済学辞典」(Dictionnaire d' conomie politique)の執筆者中最も活動的なかつ尊敬すべき人の一人であったシャール・コックラン(Charles Coquelin)は、この辞典のうち経済学(
conomie politique)の執筆者中最も活動的なかつ尊敬すべき人の一人であったシャール・コックラン(Charles Coquelin)は、この辞典のうち経済学(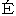 conomie politique)と題する項において、経済学の定義は未だに完成していないといった。この主張を助けるために彼は、私が既に述べたスミス、セイの定義やシスモンジ、ストルク(Storch)、ロッシ(Rossi)らの定義を示し、それらのいずれも他を排して採らねばならぬほど際立って優れていないと断言し、かつまたこれらの人は自分の著書において自分の定義に従っていないといっている。次に彼は、経済学を定義しようとする者はまずそれが科学であるか、または政策であるか、あるいはそれらの両者であるかを問うべきであり、ことに政策と科学との区別を明らかにすべきであると注意している。これはまことに明敏な注意である。この点について彼が述べている考察は目立って正しく、かつ問題は常に同じ点にあるのであるから、我々はそれを繰り返すほかはない。彼はいう、「政策は従われるべき命令または規則から成り立っている。科学は、ある現象または観察せられたまたは明らかにせられた関係の知識から成立する。政策は忠告を与え、命令し、指導する。科学は観察し記述し、説明する。天文学者が天体の運行を観察し記述するときには、科学を研究している。しかし一度この観察が終了すれば、天文学者は、航海に応用せられる規則を導き出すであろうが、この場合には政策を研究している······かように現実の現象を観察し記述する所に科学がある。命令を下し、規則を規定する所に政策がある。」
conomie politique)と題する項において、経済学の定義は未だに完成していないといった。この主張を助けるために彼は、私が既に述べたスミス、セイの定義やシスモンジ、ストルク(Storch)、ロッシ(Rossi)らの定義を示し、それらのいずれも他を排して採らねばならぬほど際立って優れていないと断言し、かつまたこれらの人は自分の著書において自分の定義に従っていないといっている。次に彼は、経済学を定義しようとする者はまずそれが科学であるか、または政策であるか、あるいはそれらの両者であるかを問うべきであり、ことに政策と科学との区別を明らかにすべきであると注意している。これはまことに明敏な注意である。この点について彼が述べている考察は目立って正しく、かつ問題は常に同じ点にあるのであるから、我々はそれを繰り返すほかはない。彼はいう、「政策は従われるべき命令または規則から成り立っている。科学は、ある現象または観察せられたまたは明らかにせられた関係の知識から成立する。政策は忠告を与え、命令し、指導する。科学は観察し記述し、説明する。天文学者が天体の運行を観察し記述するときには、科学を研究している。しかし一度この観察が終了すれば、天文学者は、航海に応用せられる規則を導き出すであろうが、この場合には政策を研究している······かように現実の現象を観察し記述する所に科学がある。命令を下し、規則を規定する所に政策がある。」一一 著者はなお註として一つの注意を与えているが、これは科学と政策との区別を完成したもので、ここに引用する価値がある。彼はいう、「我々が科学と政策との間に立てる真の区別は、人々が理論と実践との間になす区別とは何ら共通なものはない。政策の理論もあれば科学の理論もある。そして実践と矛盾することがあり得るであろうといい得るのは、政策の理論についてだけである。政策は規則を命令するが、しかしこれらの規則は一般的である。従ってこれらの命令は、たとい正しいものであっても、ある特別な場合に実践と調和し得ないと考えても不合理ではない。だが何ものをも命ぜず、何ものをもすすめず、ただ観察し説明するに止まる科学にあっては、そうではない。科学はいかなる意味においても実践と衝突することが出来ない。」
一二 コックランは政策と科学とをかく区別した後、それら各々の職分と重要さとを指摘している。彼はいう、「科学的真理が一度よく認識せられ、導き出されたとき、人間の事業の経営に適用せられるべき規則を、これらから導き出そうとするのに対して、私共は不平でもなければ、またこの
一三 しかし彼は科学と政策との間に置くべき区別を同様に強く主張し、かつこの区別を明らかにするために最後の注意を与えているが、これもまた引用の価値がある。彼はいう、「科学と政策とはしばしば多数の接触点をもっているとしても、政策と科学の範囲と輪廓とが同一であるのには、よほど多くの接触点が無ければならぬと考えられるのであって、それほどに右に述べてきた区別が強調せられる。科学が提供する理論は種々の政策によって利用せられることがあり得る。広がりの関係の学問である幾何学は、測量師・技師・砲術家・航海家・建築家の仕事を照し指導する。化学は薬剤師・染物屋・多数の工業に援助を与えている。物理学が提供してくれた一般的理論を、種々の政策がいかに利用しつつあるかを誰が正確にいい得るであろうか。反対に政策は、多くの科学によって提供せられるべき理論から光明を得ることが出来る。ただ一つの例だけを引けば医学すなわち治療の技術は解剖学・生理学・化学・物理学・植物学の理論と結果を利用している。」
一四 最後にコックランは、科学と政策との区別がいかに経済学の定義とその内容の分け方に応用せられるのに適しかつ有益であるかを、人々に感知せしめようと努力し、次いで附言していう、「科学と政策との間に今から更に純粋な区別を設け、これらの各々に異る名称を与えるように努めるべきであるか、否。私には、この区別を明らかにするだけで足るのであり、それ以上のことは、この問題をよりよく
この遠慮は意外である。極めて正当な思想をもっているこの著者が、この思想を実行に移せば与えられるであろう所の愉快と名誉とを、かくも
一五 この結果は、科学と政策とを区別する思想さえも、一見見えるようには現在の事情に適するものでないことを信ぜしめる性質を真に帯びている。しかしながら実はこの区別は経済学には完全に適用せられる。そして科学である所の富の理論すなわち交換価値及び価値の理論のあること及び政策である所の富の生産論すなわち農業・工業・商業の理論のあることを信ずるには、学派に囚われることなくわずかに反省するところがあれば足りるのである。ただここで直ちにいっておかねばならぬが、この区別に基礎があるとしても、同時にこの区別は富の分配を度外する故に、不充分である。
直ちにこの確信を得るため、経済学はある所のものの説明であると同時にあるべき所のもののプログラムであると考え得られるといったブランキの所説を想い起してみる。ところであるべき所のものは、あるいは利用または利益の観点から、あるいは公正のまたは正義の観点からのそれなのである。利益の観点からあるべき所のものは応用科学または政策の対象であり、正義の観点からあるべき所のものは道徳学または道徳の対象である。ブランキやガルニエが取扱っているのは、正義の観点から見てあるべき所のものなのである。なぜなら彼らは、経済学は道徳学であるといい、法や正義の概念を論じ、富を最も公平に分配すべき方法を論じているからである(第九節)。反対にコックランはこの見方を明らかにとっていないのであるが、ただ氏は政策と科学の区別を指摘しながら、政策と道徳との区別を指摘することを忘れている。我々はいかなるものをも見逃してはならない。我々は合理的に完全に決定的に区別をなさねばならぬ。
一六 我々は科学と政策と道徳とを相互に区別しなければならぬ。他の言葉でいえば、特に経済学、社会経済学の哲学を明らかにするために、科学一般の哲学の概要を論じなければならぬ。
科学は本体を研究するのでなくして、本体を場面として現われる事実を研究するものであることは、既にプラトーンの哲学によって明らかにせられている。本体は去り、事実は永く残っている。事実とその関係とその法則とがすべての科学的研究の目的である。そして科学は、それが研究する目的すなわち事実の差異によってのみ分かれるのである。だから科学を分けようとすれば、事実が分けられねばならない。
一七 ところでまず世界に発生する事実は二種あると考えられ得る。その一は盲目的で
一八 かようにして私は、コックランのように経験的にではなく、人間の意志の聡明と自由との考察から、科学と政策との区別を理論的に見出した。今は政策と道徳との区別を見出すことが問題である。だが人間の意志の聡明と自由とを考察しまたは少くともこの事実の一つの結果を考察すれば、社会的事実を二つの範疇に分つ原理を得ることが出来よう。
人間の意志が聡明であり自由である事実によって、宇宙のすべての存在は、人格と物との二大種類に分れる。自らを
物の目的は人格の目的に合理的に従属している。自覚を有せず自らを抑制しない物は、その目的の追求に対し、またその使命の実現に対し責任をもたない。また物は悪事も善事もなし得ないのであって、常に全く罪が無い。それは純粋の機械装置と同一視される。この点では動物も鉱物、植物と異らない。動物の衝動はすべての自然力の如く盲目的で
しかしすべての物の目的はすべての人格の目的に従属しているのではあるが、ある人格の目的は、他のいかなる人格の目的にも従属していない。もし地上にただ一人の人間しかいないとしたら、彼はすべての物を支配し得るであろう。けれども人は地上に一人ではない。地上にあるすべての人間は
一九 これによって見ると、社会事実のうちに深い区別がなされなければならぬことが解る。一方自然力に対して働きかけた人間の意志と活動から来る所のもの、すなわち人格と物との関係を区別せねばならぬ。他方他人の意志または活動に対して働く人の意志または活動から来る所のもの、すなわち人格と人格との関係を区別せねばならぬ。これら二つの範疇の事実の法則は本質的に異る。自然力に対して働く人間の意志の目的、人格と物との関係の目的は、物の目的を人格の目的に従属せしめるにある。他人の意志の領域に影響を及ぼす人間の意志の目的、人格と人格との目的は、人の使命の相互の調整にある。
故に、おそらく便利であろうと思われるが、私はこの区別を定義によって定め、第一の範疇の事実の全体を産業(industrie)と呼び、第二の範疇の事実の総体を道徳現象(moeurs)と呼ぶ。産業の理論は応用科学または政策と呼ばれ、道徳現象の理論は精神科学または道徳学と呼ばれる。
従って一つの事実が産業の範疇に属するには、またこの事実の理論が何らかの政策を構成するには、この事実が人間の意志の働きにその起源を有し、かつ物の目的を人格の目的に従属せしめるという観点から人格と物との関係を構成していなければならぬし、またこれだけで足るのである。読者は私が先に引用した政策の例を再び採ってみるなら、それらのいずれにもこの性質があることが解るであろう。例えば既に述べた建築は家の建築要素として木材及び石材を、造船は船舶建造の要素として木材及び鉄を、航海は綱具の製造、帆の据え附けまたは操縦の材料として大麻を用いる。海洋は船舶を支え、風は帆を膨脹せしめ、空と星とは航海者に航路を指示する。
一つの事実が道徳現象の範疇に属するには、そしてこの事実の理論が道徳学の一部門であるためには、この事実が常に人間の意志の働きにその起源を発し、人格の使命の相互の調整という点から見ての人格と人格との関係を成していなければならぬし、またそれだけで足りる。例えば結婚または家族等に関し、夫と妻、親と子の職分と地位を定めるものは道徳である。
二〇 科学、政策、道徳とはこのようなものである。それらのそれぞれの規準は真、利用または利益、善または正義である。さて社会的富及びそれに関係のある事実の完全な研究のうちに、この種の知的研究の一つまたは二つが材料となるものがあろうか、あるいはそれらの三つとも含まれるであろうか。これは、私が富の概念を分析しつつ次章において明らかにしようとする問題である。
[#改ページ]
第三章 社会的富について。稀少性から生ずる三つの結果。
交換価値の事実と純粋経済学について
要目 二一 社会的富は稀少な物、すなわち(一)利用があり、量において限りがある物の総体である。二二 稀少性は科学的用語である。二三、二四、二五 稀少な物のみが、またすべての稀少な物は(一)占有せられ(二)価値を有し交換し得られ(三)産業により生産し得られ増加し得られる。二六 経済学、交換価値の理論、産業の理論、所有権の理論。二七 交換価値の事実。市場において生ずる。二八「小麦は一ヘクトリットル二四フランの価値がある。」これは自然的事実である。二九 これは数学的事実でもある。 5vb=600va 三〇 交換価値は評価され得る大きさである。交換価値と交換の理論すなわち社会的富の理論は物理数学的科学である。合理的方法。代数的用語。
二一 物質的なまたは非物質的な物(物が物質であるか非物質であるかは何ら関する所ではない)であって稀少なもの、すなわち我々にとって利用があるものであると同時に量に限りがあって我々が自由勝手に獲得出来ないすべての物を社会的富(richesse sociale)と呼ぶ。
この定義は重要である。私はそれに含まれた言葉を明確にしておく。
物は何らかの使用に役立ち得るときから、すなわち何らかの欲望に
我々の各々がある物に対してもっている欲望を欲するままに満足し得るほど多くのこの物の量が存在しないとき、この物は我々の処分に対し限られた量しかないという。世には、全く無い場合を除けば、常に無限量が我々の処分に
二二 これによって、稀少(rare)と稀少性(raret
 )という語がここでいかなる意味のものであるかが解るであろう。この意味は、力学における速度、物理学における熱という語の意味の如く科学的である。数学者や物理学者にとっては速度は
)という語がここでいかなる意味のものであるかが解るであろう。この意味は、力学における速度、物理学における熱という語の意味の如く科学的である。数学者や物理学者にとっては速度は二三 (1)量において限られかつ利用のある物は、専有せられる。無用の物は、専有せられない。何らの用途にも役立たない物は、何人もこれを専有しようと思わない。また利用のある物であっても無限の量のあるものは専有せられない。まずこのような物は、無理に押し付けることも出来ねばまた差押えることも出来ない。人々はこれらの物を共有の状態から取り去ってしまうとしたところで、無限の量があるから、出来るものではない。大部分を各自の処分の下に置き得るのならとにかく、わずか一部分を所有し貯えておいて、何になるか。何かにこれを利用しようとするのか。だが、何人も常にこれを獲得出来るのに、誰がこれを需要するのか。それとも自らこれを使用するためなのであるか。だが常にいつでもこれを獲得出来ることが確実であるとしたら、これを貯蔵して何の役に立つか。空気は誰にも与えることが出来ないもので、また自ら呼吸する必要を感ずる場合には、口を開けばこれを得られるのであるから空気の貯蔵をしておく必要はない(通常の場合をいうのである)。これに反し限られた量しか存在しない利用のある物は、専有せられ得る物であり、専有せられる。まずそれらは、強制的に押しつけることも出来れば、差押えされることも出来る。ある数の個人のみが、この物の存在する量を集めて、共有の領域にこれを残しておかないようにすることが、たしかに可能である。そしてこの操作を行えば、これらの人々には二重の利益がある。第一に彼らはこれらの物の貯蔵を確保し、これらを利用して自らの欲望を充すに役立たせる可能性を準備しておく。第二にもし彼らがその貯蔵の一部しか消費しようと欲しないかまたは消費し得ないとしても、この過剰量と交換に、その代りとして消費すべきかつ量において限られた他の利用を獲得する能力を保留しておく。しかしこれはまた私共が別に取扱わねばならぬ所の異る事実となってくる。今ここでは専有(従って合法的なまたは正義に一致せる専有である所有権もまた)は社会的富にしか存在せず、またすべての社会的富に存在すると認めておくに止める。
二四 (2)利用があって量において限られた物は、先に一言触れたように、価値がありかつ交換せられ得る。稀少な物が一度専有せられると(そして稀少なもののみが専有せられ、また専有せられる物はすべて稀少である)これらすべての物の間に一つの関係が成立する。この関係とは、これら稀少な物の各々は、それに固有な直接的利用とは独立に、特別な性質として、一定の比例で他の各々と交換せられる能力をもっているということである。もし人がこれら稀少な物の一つしかもっていないとすると、これを譲渡してこれと交換に、自らもっていない他の稀少な物を得ることが出来る。そして人がこの稀少な物をもっていないとすれば、自ら所有している稀少な他の物を与えることを条件としてしか、これと交換にこの稀少な物を得ることが出来ない。もしこの物をも所有せず、またこれと交換に与えるべき何ものも
二五 (3)利用があって量において限られた物は産業により生産せられ得る物であり、または増加し得られるものである。だから規則的組織的努力によってこれらを生産し、その数を出来るだけ多く増加するのが利益である。世の中には雑草や何らの役にも立たない動物のような利用の無い物(有害な物までもいわぬとしても)がある。人々はこれらの物のうちに、これらの物を無用の範疇から有用の範疇に移さしめ得る性質がないかと、注意深く探索する。また利用はあるが量において限り無く存在する物もある。人々はこれを利用しようとはするが、その量を増加しようとはしない。最後に利用があって量において限られた物すなわち稀少な物がある。この最後のもののみが、現在の限られた量をより多くする目的をもつ研究または行動の対象となることが出来るのは明らかである。またこの最後の物は例外無くかかる研究または行動の対象となることが出来るのも明らかである。故にもし既に呼んだように、稀少な物の総体を社会的富と呼べば、産業的生産(production industrielle)または産業(industrie)は、社会的富だけにそしてすべての社会的富に行われる。
二六 交換価値、産業、所有権、これらは物の量の制限すなわち稀少性によって生ずる三つの一般的事実であり、三つの系列または種類の特種的事実である。そしてこれら三種の事実が動く場面はすべての社会的富であり、また社会的富のみである。そこで今は、例えばロッシのように、経済学は社会的富を研究するものであるというのがたとえ不正確でないとしてもいかに不明瞭で粗雑で非哲学的であるかが解るであろう。実際、経済学はいかなる観点から社会的富を研究するのであるか。その交換価値の観点、すなわち社会的富に行われる売買の現象の観点からか。または産業的生産の観点すなわち社会的富を増加することが有利であるか不利であるかの条件の観点からであるか。最後に社会的富を目的とする所の所有権すなわち専有を合法的または非合法的ならしめる条件の観点からであるか。我々はそれをいわねばならぬ。だが特に注意せねばならぬのは、これら三つまたは二つの観点から同時に研究するのではないことである。なぜなら、容易に解るように、これらの観点は各々全く異っているから。
二七 稀少な物が一度専有せられるとき、いかにして交換価値を得るかを、私共は先験的に認めた(第二四節)。一般的事実のうちに交換の事実を経験的に認めようと思えば、我々はただ眼を開きさえすればよい。
我々は皆日々、特種な一系列の行為として、交換すなわち売と買とをなしている。我々のある者は土地または土地の使用または土地の果実を売る。ある者は家または家の使用を売る。ある者は大量に獲得した工業生産物または商品を細分して売る。ある者は診療・弁護・芸術作品・ある日数または時間の労働を売る。これらを売ってこれらの人々は、貨幣を受ける。かくして得た貨幣で人々は、あるときはパン・肉・葡萄酒を
交換は市場において行われる。ある特種な交換が行われる場所を、我々は特種な市場と考える。例えばヨーロッパ市場・フランス市場・パリ市場、などという。ル・アーヴル(Le Havre)は
小麦の市場をとれば、そこで与えられた時において五ヘクトリットルの小麦が一二〇フランすなわち九〇パーセントの銀六百グラムと交換せられたとすれば、「小麦の一ヘクトリットルは二四フランの価値がある」という。これが交換価値の事実である。
二八 小麦の一ヘクトリットルは二四フランの価値がある。まずこの事実は自然的事実の性質をもっていることを注意すべきである。銀で表わした小麦のこの価値すなわち小麦のこの価格は、売手の意志から生ずるのでもなく、買手の意志から生ずるのでもなく、またこれらの二つの意志の合致から生ずるのでもない。売手はより高く売ろうとするけれども、それをなし得ない。なぜなら小麦はこれ以上の価値が無いからであり、また売手がこの価格で売らなければ、買手は、この価格で売ろうとしている他のある数の売手を見出し得るからである。また買手はより安く買おうとするがそれをなし得ない。なぜなら小麦の価値はこれ以下ではないからであり、また買手がこの価格で買おうとしなければ、売手はこの価格で買おうとするある数の買手を見出し得るからである。
故に交換価値の事実は、一度成立すれば、自然的事実の性質をもってくる。それはその起源においても自然であり、その現われにおいても自然であり、その存在の様式においても自然である。小麦や銀が価値をもっているのは、これらの物が稀少であるからであり、換言すれば利用があり、かつ量において制限せられているからであるが、これら二つの事情は共に自然的である。そして小麦と銀とが互に比較せられて、しかじかの価値を有つのは、それらがそれぞれ稀少の程度を異にするからである。他の言葉でいえば、利用の程度及び量において制限せられる程度を異にするからであるが、これら二つの事情は右に述べたそれらと同じく自然現象である。
しかしこれは、我々が価格に対し何らの働きをも加え得ない、という意味ではない。重さが自然法則に従う自然的事実だとしても、これを
二九 小麦一ヘクトリットルは二四フランの価値がある。だがこの場合にこの事実は数学的性質をもっていることを注意すべきである。銀で表わした小麦の価値すなわち小麦の価格は、昨日、二二または二三フランであった。先刻は二三・五〇フランまたは二三・七五フランであった。しばらくの後には二四・二五フランまたは二四・五〇フランとなり、明日は、二五または二六フランとなるであろう。しかし今日の現在では二四フランであって、それ以上でも無ければ、それ以下でも無い。この事実は明白に数学的事実の性質をもっているのであって、従って直ちにこれを方程式で表わすことが出来、またこの表わし方によってのみ、その真の表現をなすことが出来るのである。
ヘクトリットルは小麦の量の尺度の単位として許容せられ、グラムは銀の量の尺度の単位として許容せられたとして、もし小麦五ヘクトリットルが銀六百グラムと交換せられるとすると、正確には「小麦五ヘクトリットルは銀六百グラムに等しい価値を有する」ということも出来れば、「小麦一ヘクトリットルの交換価値の五倍は、銀一グラムの交換価値の六百倍に等しい」ということも出来る。
そこで、vb を小麦一ヘクトリットルの交換価値であるとし、 va を九〇パーセントの銀一グラムの交換価値であるとする。しからば数学の普通の記号法によって、方程式
[1] 5vb=600va
が得られ、また両辺を5で除せば、vb=120va
が得られる。もしまた、既に述べた例の中で仮定したように、一グラムの銀の交換価値の代りに、九〇パーセントの銀五グラムの交換価値を価値の尺度として採用し、かつこの銀五グラムの交換価値をフランと呼べば、換言すれば、
5va=1 フラン
であるとすれば、[2] vb=24 フラン
となる。しかし[1]の形式をとろうが、[2]の形式をとろうが、これらの方程式は、「小麦一ヘクトリットルの価値は二四フランである」という句の正確な飜訳||私はあえてこの事実の科学的表現であるといいたい||である。
三〇 故に交換価値は一つの大きさであり、評価せられ得る大きさであることを、私共は今から知ることが出来る。そして一般に数学がこの種の大きさの研究を目的とするとしたら、たしかにここに、今まで数学者が忘れていて充分に研究されていなかった数学の一分科、交換価値の理論があるわけである。
私は、この科学が経済学の全部であるとはいわない。これは既に人々が熟知している所である。力、速度は評価し得る力であるが、力と速度の数学的理論が力学の全部ではない。しかしこの純粋力学が応用力学に先行せねばならぬことも確かである。同様に応用経済学に先行する純粋経済学があり、この純粋経済学は物理数学的科学に全く相類する科学である。この主張は全く斬新であり、奇異に見えるかもしれない。しかし私は既にこの主張を証明した。私はこれを更によく証明するであろう。
純粋経済学すなわち交換価値と交換の理論、更に換言すれば抽象的に考えられた社会的富の理論が、力学・水力学の如く、物理数学的科学であるとしたら、それに数学的方法と用語とを用いるのに、何らの躊躇をする必要はない。
数学的方法は経験的方法ではなく、合理的方法である。狭義の自然科学は、自然を純粋に単純に記述するに止まり、経験の領域外に出ないものであるか。私は、この問題に答える労を自然科学者に委せておく。だがたしかなのは、物理数学的科学は狭義の数学の如くその内容のタイプを経験に借りるけれども、これらを借りたそのときから経験の領域を離れていくことである。これらの科学は現実のタイプから理念的タイプを定義し、引出してくる。そしてこれらの定義の基礎の上に、先験的に定理と証明の足場を作る。そして後その結論を応用しようとして経験に帰るのである。その結論を確証しようとして経験のうちに入っていくのではない。幾何学を多少でも学んだ者は何人も熟知するように、円の半径は互に相等しく、三角形の内角の和は二直角に等しい。だがこれは抽象的理念的円または三角形においてのみ真理である。実在は、これらの定義や証明を近似的にしか確証しない。しかもこれらの定義と証明とは充分に実在に応用され得るのである。この方法に従い、純粋経済学は、交換、需要、供給、市場、資本、収入、生産的用役、生産物等のタイプを経験に借りねばならぬ。純粋経済学は、これらの現実的形態から、定義によって理念的形態を抽象し、これら理念的形態の上に推論を行い、科学が成立してから応用を目的として再び現実に帰らなければならない。かようにして理念的市場において、理念的需要供給と厳密な関係をもつ所の理念的価格が得られる。他もすべて同様である。これらの純粋な真理はしばしば応用せられるものであろうか。厳密にいえば、科学のために科学を研究するのは、科学者の権利である。ある奇怪な図形の奇怪な性質が不思議ならば、幾何学者はこれを研究する権利をもっている(また日々この権利を行使している)。けれども純粋経済学のこれらの真理も、応用経済学及び社会経済学の上の最も重要で最も論争があったかつ最も不分明な問題に解決を与えるであろうことは、後に明らかにする如くである。
用語に関しては、数学上の用語を用いれば少数の語で最も正確に最も明快に表現出来ることをば、リカルドがしばしばなしたように、またミルが経済原論の到る所になしたように、通常の用語を用いてすこぶる不正確にすこぶる困難に説明することに人々が
[#改ページ]
第四章 産業の事実と応用経済学とについて。
所有権の事実と社会経済学とについて
要目 三一 産業の事実。直接的利用、間接的利用。利用の増加。間接的利用の直接的利用への変形。三二 産業の二系列の活動。(一)技術的活動 (二)分業の結果生ずる経済的活動。三三 二重の問題。三四 産業的経済的生産の事実は社会的事実で自然的事実ではなく、産業的事実で道徳的事実ではない。社会的富の生産の理論は応用科学である。三五 専有の事実は社会的事実であって、自然的事実ではない。自然は占有せられ得る状態を作り、人間が専有をなす。三六、三七 道徳的事実であって、産業的事実ではない。所有権は合法的な専有である。三八 共産主義と個人主義。社会的富の分配の理論は道徳科学である。三九 道徳と経済学の関係の問題。
三一 量において限られて利用がある物のみが産業により生産せられ得るのであり、またそれらはすべて産業によって生産せられる(第二五節)。そして事実において確かに、産業は稀少な物しか生産しようと努力しないし、またそれらは稀少なすべての物を生産しようと努力する。
私は、この産業的生産の事実を、今から、多少の正確さをもって明白にしておかねばならぬ。量において限られて利用がある物は、この限られているという不便のほか(これは一つの不便である)、往々にしてなお他の不便すなわち直接的利用を有しないでただ間接的利用をもっているという不便を有している。羊の毛は無論利用がある物である。しかしこれを欲望の充足例えば衣服のための欲望充足に用いるに先立って、我々はこれに、羊毛を布とする操作と、布を衣服とする操作との二つの予備的な産業上の操作を加えなければならぬ。ところで利用があるがそれが間接であり量において限られた物の数はすこぶる多いのであるが、このことはわずかに一瞬間の熟考によっても知られる。そこで産業的生産は、量において限られてしか存在しない利用がある物の量を増加する目的と、間接的利用を直接的利用に変化する目的との、二つの目的を追うものであるという結果が出てくる。
先に産業は、物の目的を人格の目的に従属せしめることを目的とする、人格と物との関係の総体であると、極めて一般的に定義しておいたが、産業の目的はかくして、正確になってくる。人間がすべての物と関係をもってくるのは、たしかに、これらの物を利用するがためである。しかしこれらの関係の不変の目的が、社会的富の増加及び変形にあることもまたたしかである。
三二 この二重の目的は、全く異る二系列の活動を通じて、人間によって追求された。
一、産業活動の二系列の一つは、狭義の産業活動すなわち技術的操作から成る。例えば農業は、食物、衣服に役立つ動植物の量を増加し、鉱業は、道具や機械を作る鉱物の量を増加する。製造工業は、繊維を絹布、毛織物、綿布に変じ、鉱物をあらゆる種類の機械に変化する。土木建築業は工場、鉄道を建設する。たしかにそれらは、物の目的を人格の目的に従属せしめようとする人と物との関係の性質を明らかにもつ活動であり、また社会的富の増加と変形を目的とするより限られたかつより確定せる性質をもっている活動である。故にそれらは応用科学または政策の対象の第一系列を構成する産業事実の第一系列すなわち技術である。
二、産業活動の第二は、狭義の産業の経済的組織に関する操作から成る。
上に述べた第一系列の活動は、第二系列の活動に見るような事実すなわち人の生理が分業に適する事実がないものとしても、産業全体を構成し技術全体の対象を構成し得よう。もしすべての人の運命が互に独立してその欲望を充足するものだとしたら、我々は各々孤立して各自の目的を追求し、無限に存在しないで利用のある物を、自ら必要と認める程度に増加し、また自ら適当と考える所に従い、間接的利用を直接的利用に変じなければならぬ。各人はあるいは百姓となり、あるいは製糸職工となり、パン屋ともなり、洋服屋ともならねばならぬ。我々の状態は動物のそれに近づいてくる。けだし狭義の産業すなわち工業は、分業に負う発展がないとしたら、些細なものに過ぎないから。しかし厳密に考えれば、この場合にも第一系列に属する産業は存在することが出来る。ただ経済的産業生産が存在し得ないのである。
実際においては、今私共が想像した如くではない。人はただに生理的に分業に適するのみならず、また後に見る如く、この適性は人間の生存と生計とに必要な条件である。すべての人の運命は、欲望の充足の観点から見ると、独立ではなくして密接な関係をもっている。今ここでは分業の事実を、その性質または起源については研究しない。先に、人の道徳的自由と人格の事実を認めただけで、それ以上の研究に入らなかった如く、ここでも今はしばらく右の事実の存在を認めておくに止める。この事実は存在するのである。各人が稀少な物を自ら増加することなく、または自己にために間接利用を直接利用に変化することなく、この仕事を各々特種の職業によって分割して行わしめるときに、この事実は成立する。ある者は特に百姓であって百姓以外のものではないし、ある者は特に製糸職工であってそれ以外の者ではないし、他の者もこれと同様である。分業の事実とはこのことである。これは、我々が社会に
三三 そこでこのことから二つの問題が生じてくる。
まず分業の無い場合と同じく、分業が行われる場合にも、社会的富の産業的生産は単に豊富でなければならぬのみでなく、またよく釣合を保っていなければならぬ。稀少なある物が過剰に増加せられていながら、他の物の量が不充分に増加せられていてはならぬ。ある間接的利用が大規模に直接的利用に変化されていながら、他の間接的利用が不充分な程度にしか直接的利用に変形せられていないようであってはならぬ。もし我々の各々が自ら百姓の仕事も、大工の仕事も、技師の仕事もするとすれば、これらそれぞれの仕事を自ら必要と信ずるだけするであろう。同様に職業が分化している場合にも、製造工業家が多過ぎて、他方百姓が少な過ぎるようなことがあってはならない。
次に、分業が行われない場合と同じく、分業が行われる場合にも、社会における人々の間に行われる社会的富の分配が、公平でなければならぬ。経済的秩序が乱れていてはならぬように、道徳的秩序が乱れていてはならない。もし我々の各々が、自ら消費する一切の物を自ら生産し、自ら生産する物しか消費しないとすれば、生産が消費の必要を目的として規制せられるのみならず、消費もまたその生産の大きさによって決定せられるであろう。ところで職業の分化があったからとて、ある者が僅少な生産をなしながら、多量の消費をなし、ある他の者が多くの多くの生産をなしながら、わずかの消費しかなし得ないようであってはならない。
かくてこれら二つの問題の重要さも了解せられ、またこれらの問題に与えられた種々なる解答の意味も了解せられ得よう。同業組合、職工組合、親方の制度は、特に生産の釣合の条件を充すことを目的としているのは明らかである。商工業自由の制度すなわち普通にレッセ・フェール、レッセ・パッセの制度と呼ばれるものは、釣合の条件と、富を豊富ならしめる条件とをよく調和しようとする主張をもっている。この制度に先行した奴隷制度、農奴の制度は、社会のある階級をある他の階級の利益のために労働せしめたという不便を明らかにもっていた。現在見る如き所有権及び租税の制度は、人間による人間の搾取を完全に廃止したといわれる。私共は後にそれを検しよう。
三四 今はただ二つの問題の存在を認め、次にそれらの目的を確定した後、それらの性質を精確にするという一つの事をなすに止める。さてコックランとその派の経済学者がいかにいおうと、社会的富の生産問題にはもちろん、その分配問題にも、自然科学の問題の性質を与えることはまずもって不可能である。人の意志は、社会的な生産の事実に対しても、分配の事実に対しても、自由に働く。ただ分配の場合には、人の意志は正義を考慮して働き、生産の場合には利益を考慮して働く。実際技術的産業の事実と私が右に定義したような経済的生産の事実との間には、性質の相異はない。二つの事実は相互に関係をもっていて、一方は他方を補完する。二つは共に人間的事実であって自然的事実ではない。かつ二つは共に産業的事実であって道徳的事実ではない。けだし二つは共に、物の目的を人格の目的に従属せしめることを目的とする人格と物との関係から成立しているから。
故に社会的富の経済的生産の理論すなわち分業を基礎とする産業組織の理論は応用科学である。我々がそれを名附けて応用経済学(
 conomie politique appliqu
conomie politique appliqu e)というゆえんはここにある。
e)というゆえんはここにある。三五 既に明らかにしたように、量において限られて利用がある物のみが専有せられ、またこのような物はすべて専有せられる(第二三節)。そしてこのような物のみが専有せられ、またこのような物がすべて専有されていることは、ただ我々の周囲を眺めれば、直ちに認められる。利用の無い物[#「物」は底本では「者」]は見捨てられ、利用があっても量において無限な物は、共有の領域に見捨てられる。これに反し稀少な物は引込められていて、最初に来る人といえどももはやこれを自由にすることが出来ない。
稀少な物すなわち社会的富の専有は人間的事実であって、自然的事実ではない。その起源は人間の意志と行動にあって、自然力の活動にあるのではない。
利用があって量において無限な物が専有せられることがあっても、もちろんそれは我々によるのではない。また利用があって量において限られた物が専有せられないことがあっても、もちろんそれは我々によるのではない。しかし専有の自然的条件が一度充されれば、この専有はある仕方で行われ、他の仕方では行われないというのは、我々によるのである。もちろんそれは個々の人によるのではなく、我々の全体によるのである。それは、各人の個人的意志にその起源を有する人間的事実である。実に人の創意は、専有の事実を欲するままに修正するように、この事実に対し過去において働いたのであり、現在働きつつあり、また働くであろう。社会の成立の当初においては分業を行った人々の間の物の専有すなわち社会的富の分配は、合理的条件を全く離れて行われたのではないにせよ、おおむね力に制せられ、策略に制せられ、偶然に制せられて行われた。最も大胆[#「大胆」は底本では「大謄」]な者、最も強い者、最も巧妙な者、最も好運な者が最もよい分け前を得、他の者はその残部を、すなわち僅少な物を得たか、またはほとんど全く何ものも得ていなかったのである。しかし政治と同じように所有権もまた、当初の無秩序な事実から、秩序ある最後の原理へと、徐々に進んできた。要するに自然は専有せられ得る状態を作ったのに止り、専有の状態を作ったのは人間である。
三六 かつまた、人間による物の専有すなわち社会の人々の間における社会的富の分配は、道徳的事実であって、産業的事実ではない。人格と人格との関係である。
もちろん我々は、稀少な物を専有しようとする目的をもって、これらの物との関係に入るのである。そして長い継続的努力の後にしか、この専有の目的を達し得ない場合も少くない。しかしこの観点、既に述べた所のこの観点をここでは採らない。今はただ予備的事情や自然的条件に関係なく、社会における人間の間の社会的富の分配の事実を考えよう。
私は、野蛮人の一族と森林中にいる一匹の鹿とを想像する。この鹿は量において限られて利用がある物であり、従って専有せられる。私はこの点を疑の無いものと考えて論じない。しかしいわゆる専有をなすに先立って、この鹿を追い殺さねばならぬ。私は問題の第二面であるこの点も論じない。これは狩猟の問題であって、この鹿を切断し煮焼するのが料理の問題であるのに等しい。だが鹿とのこれらの関係を捨象しても、なお一つの問題がある。それは、森林中に鹿がいたとき、または死んだとき、誰がこれを専有するかの問題である。問題となるのは、このように見られた専有の事実である。また人と人との関係を構成するものは、このように見られた専有の事実である。そしてこの問題に一歩を踏み入れれば、我々は直ちに次の事実を信ぜざるを得ない。||「一族中の若年の機敏な一人がいう。鹿は、これを殺した者が専有すべきである。諸君が
三七 かようにして専有の形態は我々の決断に依存するのであり、採られた決断がよいか悪いかに従って、専有の形態はあるいはよいものとなり、あるいは悪いものとなる。よい形態であれば、人々の使命をこれらの人々の間によく調和せしめ、正義の要求を満足せしめるであろう。悪い形態であれば、ある人の使命をある他の人々のそれに従属せしめ、不正義を生ぜしめるであろう。いかなる形態が良いものであってかつ正当なのであるか。いかなる形態の専有が、道徳的人格の要求に合うものとして理性によって推薦せられるものであるか。ここに所有権の問題がある。所有権は公正で合理的な専有であり、合法的な専有である。専有は純粋にして単純な事実である。所有権は合法的事実であり、権利である。事実と権利との間には、道徳論の余地がある。ここに本質的な点があるのであって、これを誤解してはならない。専有の自然的状態を明らかにし、あらゆる所と時において社会の人々の間に社会的富の分配が行われている種々な形態を枚挙してみたところで、それは何ものでもない。これらの形態を、道徳的人格の事実から出てくる正義の観点から、また平等と不平等の観点から批評し、それらがいかなる点に常に欠陥があったかを指摘し、唯一の良い形態を示すこそ、すべてである。
三八 社会的富と、社会を作っている人とが現れて以来、社会の人々の間における社会的富の分配の問題は論議されてきた。それは常に正しい、そしてその上に分配を維持しなければならない基礎を問題としてきた。考え出されたすべてのシステムのうちで最も有名なのは、古代の最大の哲学者プラトーンとアリストートをチャンピオンとする共産主義と個人主義である。だが共産主義といい、個人主義といい、それらは何を意味するか。共産主義者はいう、「財は共同に専有せられねばならぬ。自然は財をすべての人に与えた。単に現に生存している人にのみならず、将来生存するであろう人々にも与えたのである。これを個々の人々の間に分つのは、現存の社会と後世の社会の財産を分割することである。それは、この分割後に生れる人々をして、神が準備してくれた資源を利用出来ないようにすることである。これらの人々の目的の追求とその使命の実現を妨げることである。」これに対し個人主義者は答える。「財は個人によって専有せられねばならぬ。自然は人々を、各々の徳につき、
 conomie sociale)である。
conomie sociale)である。三九 だがここに一つの困難がある。私はそれを指摘しておきたいと思う。
所有権の理論は、道徳的人格としての人間と人間との間に存在する社会的富に関する関係、すなわち社会における人々の間の社会的富の公正な分配の条件を決定する。産業の理論は、特種な職業に従事して労働者と考えられる人と物との関係を、社会的富の増加と変形の観点から決定する、すなわち社会の人々の間に社会的富を豊富ならしめる条件を決定する。前者の条件は、正義の観点から導き出されるべき道徳的条件である。後者の条件は、利益の観点から導き出されるべき経済的条件である。しかしこれらは同じく社会的条件であり、社会の組織を目的とする手引きである。ところでこれら二つの種類の考察は互に矛盾するのであるか、または反対に相互に支持し合うのであるか。例えば所有権の理論と産業の理論とが共に奴隷制度または共産主義を拒否したとしても、もちろんよい。しかしこれらの理論の一つが、正義の名によって奴隷制度を拒否し、または共産主義を吹聴し、他の一つは、利益の名をもって、奴隷制度を賞讃し、または共産主義を拒否したと想像すれば、道徳科学と応用科学との間に矛盾があることになる。この矛盾は可能であるか。この矛盾が現れたとしたら、いかになすべきであろうか。
我々はこの問題に遭遇するのであるが、私はこの問題に、それがもつべき地位を与えたいと思う。これは特にプルードンとバスチアとの間に、一八四八年の頃、道徳と経済学の関係について行われた論争の問題であった。プルードンは「経済的矛盾」において、正義と利益との間に矛盾があると主張し、バスチアは「経済的調和」において反対の説を主張した。私は二人が共にその証明を完全に果したとは考えない。そして私はバスチアの説を採るが、しかしバスチアとは異る方法によってこれを弁じたいと思う。とにかく、問題が存在するとしたら、これを解決せねばならない。全く異る道徳科学である所有権の理論と、応用科学である産業の理論とを混同して、この問題を
[#改丁]
第二編 二商品間に行われる交換の理論
[#改丁]
第五章 市場と競争とについて。二商品間に行われる交換の問題
要目 四〇 社会的富は価値がありかつ交換し得られる物のすべてである。四一 交換価値は互にある割合の分量で受けまたは与えられる物がもつ性質である。市場は交換が行われる場所である。競争の機構の分析。四二、四三 証券市場。有効な需要と供給。供給と需要の均等、静止的な流通価格。需要が供給に超過すれば騰貴する。供給が需要に超過すれば下落する。四四 商品A及びB。方程式 mva=nvb. 価格 pa 及び pb. 四五 有効な需要と供給、Da, Oa, Db, Ob. 定理 Ob=Dapa, Oa=Dbpb. 需要が主要な事実であり、供給は附随的な事実である。四六 定理  . 四七 供給と需要の均等すなわち均衡の仮説。四八 供給と需要の不均等の仮説。価格の騰貴または下落は需要を減少、または増加せしめる。供給については
. 四七 供給と需要の均等すなわち均衡の仮説。四八 供給と需要の不均等の仮説。価格の騰貴または下落は需要を減少、または増加せしめる。供給については如何 。
 . 四七 供給と需要の均等すなわち均衡の仮説。四八 供給と需要の不均等の仮説。価格の騰貴または下落は需要を減少、または増加せしめる。供給については
. 四七 供給と需要の均等すなわち均衡の仮説。四八 供給と需要の不均等の仮説。価格の騰貴または下落は需要を減少、または増加せしめる。供給については四〇 第二一節になした基礎的一般的考察の中で、私は、社会的富を、稀少な物すなわち利用があると同時に量において限られた有形または無形の物の総体であると定義し、かつ稀少な物はすべて、そしてこれらのみが価値があり、交換せられ得ることを証明した。それとは別にここでは、社会的富を価値があって交換せられ得る有形無形の物の総体であると定義し、かつ価値があって交換せられるすべての物が、そしてそれらのみが利用があると同時に量において限られている物であることを証明しよう。先の定義では、私は原因から結果に赴いているわけであり、今与えた定義では、結果から原因に遡っているわけである。だが稀少性と交換価値との二つの事実の関係を明らかにすることが出来るならば、これらのいずれの行き方をしようと、自由であるのはいうまでもない。ただ私は、交換価値のような一般的事実の組織的研究にあっては、性質の研究が起源の研究に先立たねばならぬと考えるのみである。
四一 交換価値はある物がもつ性質であり、無償で獲得せられることも無償で譲渡されることもなくして売り買いせられる性質、すなわち他の物を与えまたは受けるのにある割合の分量で受けまたは与えられる性質である。一つの物の売手は、それと交換に受ける物の買手である。一つの物の買手は、それと交換に与える物の売手である。他の言葉でいえば、二つの物の相互の交換はすべて二つの売りと買いとから成り立つ。
価値があって交換せられる物は、また商品(marchandises)と呼ばれる。市場は商品が交換せられる場所である。故に交換価値という現象は市場に生れるのであって、交換価値の研究は市場においてなされねばならぬ。
自由に放任せられる限り、交換価値は自由競争の支配を受けている市場において自然に発生する。交換をなす者は、買手としては互により高く需要しようとし、売手としては互により安く供給しようとする。これらの競り合いから、あるいは上向の、あるいは下向の、あるいは静止する商品の交換価値が生れる。この競争が充分に働くか否かによって、交換価値は、あるいは正確に、あるいは不正確に現われる。競争の点から見て最もよく組織化された市場は、売買が例えば仲買人・才取等のような売買を集中する仲介者によって行われる市場である。従ってこのような市場では、いかなる交換も、その条件が公にせられることなくしては行われず、売手が互により安く売ろうとし、買手が互により高く買おうとすることなくしては、行われない。株式取引所・商品取引所・穀類取引所・魚市場等は、実にこのような働き方をする市場である。しかしこれらの市場のほかに、多少は制限せられていても競争がともかくも相応にかつ満足な程度に行われる市場がある。
四二 ところでよく組織せられた市場において競争がいかに働くかを見ようと思うのであるが、その目的のために、パリまたはロンドンのような資本の大市場における証券取引所に入ってみよう。これらの場所で人々が売買している物は、社会の富のうちで、証券によって表わされている重要な富の一部分である。例えば国家その他の公共団体に対する債権の一部分・鉄道・運河・重工業工場等の一部分である。我々がこの市場に入るとき、聞き得るものは、取りとめのない喧騒のみであり、見得るものは、無秩序の運動のみである。しかし一度私共がその内容に通暁するに至るならば、この喧騒とこの活動との意味が極めて明瞭になってくる。
今例えばパリの取引所において行われる三分利付フランス国債の取引を、他の取引から引離して観察してみる。
三分利付公債は六〇フランであるという。これを六〇フランまたはそれ以下に売ってよいとの指図を受けた仲買人は、三分利付の公債のある量すなわちフランス国家に対する三分の利子の要求証券のある量を六〇フランの価格で供給する。かくの如く一定の価格である量の商品が供給せられたとき、この供給を有効供給(offre effective)と呼ぶ。反対に六〇フランまたはそれ以上で買ってもよいとの指図を受けた仲買人は、三分利付公債のある量を六〇フランの価格で需要しているのである。ある価格である量の商品が需要せられるとき、この需要を有効需要(demande effective)と名づける。
さてこの需要が供給に等しいか、これより多いかまたは少いかに従って、我々は三箇の仮定を設ける。
仮定一。六〇フランで需要せられる量が、この価格で供給せられる量に等しい場合。これは売手または買手である仲買人がいわばその相手方を他の買手または売手である仲買人に正確に見出す場合である。この場合には交換が行われ、相場は六〇フランを維持し、市場の静止状態すなわち市場の均衡(
 quilibre)が現われる。
quilibre)が現われる。仮定二。買手である仲買人がその相手方を見出し得ない場合。この場合には六〇フランの価格で需要せられる三分利付公債の量は、この価格で供給せられる量を超過している。理論上交換は中止せられる。六〇・〇五フランまたはそれ以上で買ってもよいとの指図を受けた仲買人がこの価格で需要する。彼らはせり上げる。このせりは二つの結果を生ぜしめる。(一)六〇・〇五フランでの買手となり得ない所の六〇フランの買い手は退く。(二)六〇フランでの売手となり得ない所の六〇・〇五フランにおいての売手が加わってくる。もし彼らが既に指図を与えていないとすれば、彼らは新に指図を与える。かく二つの動因によって、有効需要と有効供給との間に存する隔りは減少する。両者の均等が再び出現すれば、価格の騰貴はそこで停止する。そうでない場合には六〇・〇五フランから六〇・一〇フランに、六〇・一〇フランから六〇・一五フランにと、供給と需要との均等が成立するまで、価格は騰貴する。そして高い相場で、新しい静止状態が現われる。
仮定三。売手である仲買人がその相手方を見出し得ない場合。この場合には六〇フランの価格で供給せられる三分利付公債の量は、同じ価格で需要せられる量より大である。この場合にも交換は停止する。五九・九五フランまたはそれ以下で売ってもよいとの指図を受けた仲買人は、この価格で供給する。彼らは互にせり下げる。
これから二つの結果が生ずる。(一)五九・九五フランにおいて売手となり得ない所の六〇フランにおいての売手は退く。(二)六〇フランにおいて買手となり得ない所の五九・九五フランにおいての買手が現われる。そこで供給と需要との隔りが減少する。そして供給と需要との均等が再び現われるまで、価格は五九・九五フランから五九・九〇フランへ、五九・九〇フランから五九・八五フランへと下落する。
この三分利付フランス国債に行われたと同じ作用が、すべての公債例えばイギリス、イタリア、スペイン、トルコ、エジプト等の公債にも、また鉄道・港湾・運河・鉱山・
四三 私共は、これからかかる競争状態において生ずる交換価値を研究しようとする。一般に経済学者は、例外的な事情の下に現われるような交換のみを研究しようとする。彼らはダイヤモンドや、ラファエルの絵画、流行の音楽会のみを研究する。ジョン・スチュアート・ミルの引用によれば、ド・クィンシー(De Quincey)氏は、汽船に乗ってスーペリオール湖(Lac Sup
 rieur)を旅行する二人を想像する。一人は楽器を所有し、他の一人は「文明から八百
rieur)を旅行する二人を想像する。一人は楽器を所有し、他の一人は「文明から八百四四 交換の現象と競争の機構の基本概念を与えるため、私は、株式市場において金銀貨幣と交換せられる証券の売買を例にとった。けれどもこれらの証券は全く特殊な種類の商品であり、交換に貨幣が介在するのもまた交換の特殊の場合である。私は後に貨幣が介在する交換の研究をするが、当初にはこれを交換価値の一般的事実の研究と混同せぬがよいように思う。そこで私共の本道に立ち帰り、かつ私共の観察に科学的性質を与えるため、任意の二商品のみをとることとする。今これらの二商品を、燕麦と小麦であると仮定してもよければ、または抽象的に(A)、(B)と仮定してもよい。私はA、Bを(A)、(B)のように括弧に収め、量を表わす文字との混同を避けたい。量を表わす文字は方程式に組み込まれる唯一のものであり、(A)、(B)で表わすものは量ではなくして、種類であり、哲学上の言葉を用いれば、本質である。
そこで今、一市場を想像し、そこに(A)を携えながらその一部分を与えて(B)を得ようとする人々が一方から到着し、(B)を所有しその一部分を与えて(A)を得ようとしている人々が他方から到着したとする。この場合にせりの基礎となるものが必要であるから、今は例えば、ある仲買人が、前回の取引の相場通り、(A)のm単位に対し(B)のn単位を与えると想像する。この交換は次の方程式で表わされる。
mva=nvb
ここで(A)の一単位の交換価値を va と呼び、(B)の一単位の交換価値を vb と呼んでおく(第二九節)。交換価値の比すなわち相対的交換価値を価格(prix)と一般的に呼び、(A)で表わした(B)の価格、(B)で表わした(A)の価格を、それぞれ pb, pa で一般的に表わし、比


価格すなわち交換価値の比は、交換せられた商品の量の反比に等しい。
各商品の価格は互に逆数である。
もし(A)が燕麦であって、(B)が小麦であるとし、仲買人が五ヘクトリットルの小麦を一〇ヘクトリットルの燕麦と交換しようと申込んだとすれば、燕麦で表わした小麦の申込価格は2であって、小麦で表わした燕麦の申込価格は
四五 価格
 における(A)及び(B)の有効需要及び有効供給を、それぞれ Da, Oa, Db, Ob とすれば、これらの需要量と供給量と価格との間には、ここに指摘しておかねばならぬ重要な関係がある。
における(A)及び(B)の有効需要及び有効供給を、それぞれ Da, Oa, Db, Ob とすれば、これらの需要量と供給量と価格との間には、ここに指摘しておかねばならぬ重要な関係がある。先にいったように、有効需要及び有効供給は一定の価格における一定商品量の需要及び供給である。故に pa の価格において、(A)の Da 量の需要があるといえば、それは、Dapa に等しい Ob 量の(B)が供給せられているということである。だから例えば小麦で表わした価格
Ob=Dapa
が成立する。同様に pa の価格で Oa 量の(A)の供給があるといえば、それは、Oapa に等しい Db 量の(B)が需要せられるということでもある。だから例えば小麦で表わした価格
Db=Oapa
同様に Db, Ob, pb, Oa, Da の間に、次の方程式が成立するのを証明し得るであろう。Oa=Dbpb
Da=Obpb
これら二つの式は、先の二つの方程式と方程式 papb=1 とからも導き出されるが、それに関係なく証明せられ得る。Da=Obpb
よって、ある商品を反対給付とする一商品の有効需要または供給は、このある商品の有効供給または有効需要と、この一商品で表わされたこのある商品の価格との積に等しい。
ここで、これら四つの量 Da, Oa, Db, Ob のうち、二つは他の二つから決定せられることを、知ることが出来る。私共は、後に新しい説明を加えるまで、供給量 Ob 及び Oa は、需要量 Da 及び Db から生ずるものであると考え、需要量が供給量から生ずるものとは考えないでおく。実際二つの商品の相互の物々交換の現象においては、需要は根本的な事実であると考えられねばならぬし、供給は附随的な事実であると考えられねばならぬ。人は供給のために、供給するのではない。供給をすることなくしては、需要をすることが出来ない故に、供給をするのである。供給は需要の結果に過ぎない。故にまず我々は、供給と価格との間に間接的関係を認めるだけで満足し、需要と価格との間にのみ直接の関係を求めようと思う。これ故、pa, pb の価格において、Da, Db の需要があるとすれば、供給は
Oa=Dbpb, Ob=Dapa
となる。四六 ところで、
Da=αOa
であるとすれば、α=1 であるか、α>1 であるか、α<1 であるかの三つの仮定を設けることが出来る。だがまず最後の定理を述べておく。上記の方程式に、
Da=Obpb
Oa=Dbpb
によって与えられた Da, Oa の値を代入すれば、Oa=Dbpb
Ob=αDb
となる。よって、二つの商品を与えられたとすれば、一つの商品の有効需要のその有効供給に対する比は、他方の商品の有効供給の有効需要に対する比に等しい。
この定理は次のように証明せられることも出来る。
Da=Obpb
Db=Oapa
Db=Oapa
DaDb=OaOb
または、Oa=Dbpb
Ob=Dapa
OaOb=DaDb
結局、いずれの考え方によるもOb=Dapa
OaOb=DaDb

故に(A)の有効需要と供給とが等しければ、(B)の有効供給と需要ともまた等しいことが解る。もし(A)の有効需要がその有効供給より大であれば、(B)の有効供給は同じ比例で有効需要より大であることが解る。最後にもし(A)の有効供給が有効需要より大であれば、(B)の有効需要は同じ比例でその有効供給より大であることが解る。これが右の定理の意味である。
四七 さて α=1, Da=Oa, Ob=Db であると仮定すれば、二商品(A)、(B)がそれぞれ
 の価格で需要せられる量、供給せられる量は相等しい。各々の買手及び売手は売手または買手にちょうどその相手方を見出す。従って市場の均衡が現われる。均衡価格
の価格で需要せられる量、供給せられる量は相等しい。各々の買手及び売手は売手または買手にちょうどその相手方を見出す。従って市場の均衡が現われる。均衡価格四八 しかし
もちろん、Da が Oa より大であれば、pa は騰貴せねばならぬ。(すなわち pb は下落せねばならぬ。)また反対にもし、Db が Ob より大であるとすれば、pb は高騰せねばならぬ。(pa は下落せねばならぬ。)需要についても同様の推論をなし得る。すなわち価格が騰貴すれば、需要は増加することが出来ない、減少せざるを得ない。実際例えば一〇ヘクトリットルの燕麦に対し、五ヘクトリットルの小麦を供給する交換者、すなわち小麦で表わした価格 0.50 で一〇ヘクトリットルの燕麦を需要する交換者が、一二ヘクトリットルの小麦の所有者であるとする。小麦で表わした燕麦の価格 0.50 では、この交換者は二四ヘクトリットルの燕麦を買い得る。しかし彼は、小麦に対する欲望の事情で、一〇ヘクトリットルしか買わないとする。価格が 0.60 だとすると、二〇ヘクトリットルの燕麦しか買い得ない。この場合には、彼は、小麦に対する欲望の事情で、たかだか一〇ヘクトリットル||彼が更に富んだときにはこの量に達し得ようが||またはそれ以下にこれを限るであろうと、考えられねばならぬ。かくの如く、pa の高騰すなわち pb の下落は、Da を減じ、Db を増加せしめることしか出来ない。反対に pb の騰貴すなわち pa の下落は、Db を減じ、Da を増加することしか出来ない。しかし Oa と Ob とはいかに変化するか。この問に答えるのは不可能である。Oa は Db と pb との積に等しい。ところでこれら二つの因子の一方の pb が減じまたは増大すれば、他方の因子の Db は、このことだけで増加しまたは減少する。同様に Ob は Da と pa との積に等しい。ところで pa が増加するか減少するかに従って、Da は、このことだけで、減少しまたは増加する。従って、交換者が均衡を実現するか否かを、いかにして知るべきかが問題となる。
[#改ページ]
第六章 有効需要曲線と有効供給曲線。需要と供給との均等の成立
要目 四九 価格の増加に応じて有効需要が減少するという事実。五〇、五一、五二 価格の函数としての部分的需要の曲線または方程式。五三 需要曲線は同時に供給曲線である。五四 存在量の双曲線。五五 座標軸と存在量の双曲線との間における需要曲線の中間的位置。五六 二商品相互間の交換の問題の解。五七 需要曲線の中に底辺が互に逆数であり、高さがそれぞれの面積に反比例する矩形 を挿入することによる幾何学的解。五八 代数的解。五九 価格の関数としての供給曲線を構成することによる二つの解の結合。六〇、六一 有効需要供給の法則すなわち均衡価格成立の法則。
四九 ここでは、価格と有効供給との間には間接の関係しかなく、価格と有効需要との間にのみ直接の関係があると考えるのであるから、我々が研究せねばならぬのは後者である。
この研究のために、ここに小麦の所持者があるとする。この人は小麦を所有するが、燕麦を所有しない。そこで自分の消費のために、若干量の小麦を保留し、他の若干量の小麦を提供して、自家の馬を養うための燕麦と交換しようとしている。ところで彼が保留しようとする量及び提供しようとする量は、それぞれ燕麦の価格と、この価格で彼が需要しようとする燕麦の量に依存するであろう。いかに依存するか。私はそれを見ようと思う。価格零のとき(燕麦の一ヘクトリットルを得るために、小麦のゼロヘクトリットルを与えることを要するとき、すなわち燕麦が無償であるとき)、この人は欲するだけの燕麦を需要するであろう。換言すれば、自分が所有する一切の馬、否飼料が無償で得られるときに養われるべき一切の馬を飼養するに充分な量を需要するであろう。いうまでもなく彼は、これと交換に小麦を与えるのではない。次に価格が順次に
 だとすると(燕麦一ヘクトリットルを得るために、小麦
だとすると(燕麦一ヘクトリットルを得るために、小麦 を与えねばならぬとすると)、彼は次第にその需要を減ずるであろう。価格が 1, 2, 5, 10(燕麦一ヘクトリットルを得るために小麦 1, 2, 5, 10 を与えねばならぬとすれば)となれば、彼は更にその需要を減ずるであろう。そしてもちろんこれらと交換に彼が供給する小麦の量は、彼が需要する燕麦の量とこの燕麦の価格の積に常に等しい。更にまた価格が 100 というような高いものとなれば(一ヘクトリットルの燕麦を得るため 100 ヘクトリットルの小麦を与えることを要するとすれば)彼は少しの燕麦をも需要しないようになる。なぜならこの価格においては二頭の馬をも飼養し得ないであろうし、また飼養するを欲せぬであろうから。このときには、彼は、交換に何らの小麦をも供給しないであろうことは、いうまでもない。故に燕麦の有効需要は、価格が増加するに従って減少する。それは価格零においてのある数字に始まり、ある価格において零に終る。これに相応ずる小麦の有効供給は零から出発し、次第に増加し、最大に達し、再び零に帰る。
を与えねばならぬとすると)、彼は次第にその需要を減ずるであろう。価格が 1, 2, 5, 10(燕麦一ヘクトリットルを得るために小麦 1, 2, 5, 10 を与えねばならぬとすれば)となれば、彼は更にその需要を減ずるであろう。そしてもちろんこれらと交換に彼が供給する小麦の量は、彼が需要する燕麦の量とこの燕麦の価格の積に常に等しい。更にまた価格が 100 というような高いものとなれば(一ヘクトリットルの燕麦を得るため 100 ヘクトリットルの小麦を与えることを要するとすれば)彼は少しの燕麦をも需要しないようになる。なぜならこの価格においては二頭の馬をも飼養し得ないであろうし、また飼養するを欲せぬであろうから。このときには、彼は、交換に何らの小麦をも供給しないであろうことは、いうまでもない。故に燕麦の有効需要は、価格が増加するに従って減少する。それは価格零においてのある数字に始まり、ある価格において零に終る。これに相応ずる小麦の有効供給は零から出発し、次第に増加し、最大に達し、再び零に帰る。五〇 小麦のすべての所有者はもちろん、また一方のこれら小麦のすべての所有者のみならず、他方の燕麦のすべての所有者もまた、同一の性質とはいい得ないとしても、同様の傾向をもっている。一般に商品を所有してこれを他の商品と交換しようとして市場に現われる者は、せり上げの傾向をもっている。この傾向は可能的(virtuelle)であることもあり、有効(effective)であることもあるが、精密に決定せられ得べきものである。
(B)の qb 量の所有者(1)が||以下代数記号で呼ぶ||市場に現われ、そのうちのある量 ob を供給して、自分が需要する(A)の da 量と交換するとすれば、方程式
dava=obvb
により、彼は(A)の da 量と(B)の を所持して帰っていくであろう。そしていかなる場合にも、量 qb,
を所持して帰っていくであろう。そしていかなる場合にも、量 qb, qb=y+dapa
qb の所有者が qb を知っているのは、いうまでもない。しかし市場に到着してみなければ、qb の所有者が自ら市場に現われる場合には、せり上げの傾向を有効ならしめないで、可能的ならしめることが出来る。他の言葉でいえば、価格 pa が決定した後に至って初めて、需要 da を決定することが出来る。しかしその場合にもせり上げの傾向はもちろん働く。またもし例えば彼が自ら市場に現われることが出来ず、ある理由により、ある友人または仲買人に指図を与えるとすれば、彼は pa の可能な値を零から無限大まで予想し、それらに相応する da のすべての値を決定し、これを何らかの方法で表現しておかねばならぬ。ところで、計算に少しく馴れた人々は右の事実の数学的表現をなすのに二つの方法があるのを知っているであろう。

五一 第一図において、横軸 Op を価格を示す軸とし、縦軸 Od を需要を示す軸とする。原点Oから横軸上にとられた長さ Opa', Opa'' ······は、(B)で表わした(A)の価格、例えば小麦で表わした燕麦の可能な種々の価格を示すものとする。同じ原点Oから縦軸にとった長さ Oad,1 は、価格が0のとき、小麦または(B)の所有者が需要する燕麦または(A)の量を示すものとする。点 p'a, p''a ······を通って需要軸に平行線を引いて、これらの平行線の上にこれらの点 p'a, p''a ······からとった長さ p'aa'1, p''aa''1 は、それぞれ p'a, p''a の価格で需要せられる燕麦または(A)の量を示す。長さ Oap,1 は小麦または(B)の所有者が燕麦または(A)をもはや需要しないであろう価格を示す。
そうとすれば、(B)の所有者(1)のせり上げる傾向は、幾何学的には、点 ad,1, a'1, a''1 ··· ap,1 によって作られる曲線 ad,1 ap,1 により、代数的には、この曲線の方程式
da=fa,1(pa)
によって表わされる。曲線 ad,1ap,1 と方程式 da=fa,1(pa) とは経験によって得られる。同様にして、(B)のすべての所有者(2)、(3)······のせり上げの傾向を、幾何学的には曲線 ad,2ap,2, ad,3ap,3 ······により、代数的には、da=fa,2(pa),da=fa,3(p[#「p」は底本では「d」]a) ······
によって表わすことが出来る。
五二 さて、同じ横坐標の上にあるすべての縦坐標を加えて、いわばこれらの部分的曲線(courbes partielles)ad,1ap,1, ad,2ap,2, ad,3[#「d,3」は底本では「d3」]ap,3[#「p,3」は底本では「p3」] ···を合計すれば、すなわち同一の横坐標におけるすべての縦坐標を加えれば、(B)のすべての所有者のせり上げの傾向を幾何学的に示す全部曲線 AdAp(第二図)が得られる。同様にすべての部分的方程式を加えれば、同じせり上げの傾向を代数的に示す全部方程式
Da=fa,1(pa)+fa,2(pa)+fa,3(pa)+ ··· =Fa(pa)
が得られる。これらは、(B)で表わした(A)の価格の函数としての(A)の((B)を反対給付とする)需要曲線(courbe de demande)または需要方程式( quation de demande)である。同様にして、(A)で表わした(B)の価格の函数としての(B)の((A)を反対給付とする)需要曲線または需要方程式が得られる。
quation de demande)である。同様にして、(A)で表わした(B)の価格の函数としての(B)の((A)を反対給付とする)需要曲線または需要方程式が得られる。ここで、部分的曲線 ad,1ap,1 または部分的方程式
da=fa,1(pa)
を初めとし、他の部分的曲線及び方程式が連続であること、すなわち pa の無限小の増加が da の無限小の減少を生ぜしめることを、何ものも示していない。否反対に、これらの函数はしばしば不連続である。例えば燕麦についていえば、小麦の所有者の第一人は価格が騰貴するに従って、燕麦の需要を減ずるのではなく、たしかに、彼が畜舎に飼養する馬を減じようとするときに、断続的にその需要を減ずるのである。故に彼の部分的需要曲線は、実際においては、a 点を通る階段形の曲線の形(第一図)をとるのである。他のすべての人の曲線もいずれも同様である。しかし全部曲線 AdAp(第二図)は、いわゆる大数の法則によって、ほぼ連続であると考え得られる。まことに、価格の極めて小さい騰貴が起るときには、多数の人々のうちおそらく一人くらいは、今まで飼養していた馬のうち一頭を手放すような極限に立っていて、需要を減ずるであろうが、この減少は全需要中の極めて小なる部分の減少に過ぎないであろう。五三 このようにして、曲線 AdAp は、(A)の価格の函数としての(A)の有効に需要せられる量を示す。例えば Am 点の横坐標 Opa,m によって表わされる価格 pa,m における有効需要は、同じ点 Am の縦坐標 ODa,m によって表わされる Da,m である。そして(B)をもってする(A)の有効需要が、価格 pa,m であるとき、Da,m であれば、(A)と交換に提供せられる(B)の有効供給は、このことだけで、
Ob,m=Da,mpa,m(第四五節)
となる。これは縦坐標 ODa,m と横坐標 Opa,m によって作られる矩形 ODa,mAmpa,m によって表わされる。だから曲線 AdAp は(B)で表わした(A)の価格の函数としての(A)の需要と(B)の供給とを同時に示している。同様に曲線 BdBp は(A)で表わした(B)の価格の函数としての(B)の需要と(A)の供給とを同時に示すのである。五四 (B)を所有する多数者の手中にあって市場に現われた総量を Qb とし、点 Qb を通る曲線を、xy=Qb を方程式とする直角双曲線であるとする。直線 pa,mAm を、この双曲線との交点 Qb まで延長し、x軸すなわち価格の軸に平行線 βQb を引け。しからば矩形 OβQbpa,m の面積 Qb は、市場に
Qb-Da,mpa,m
は、同じ価格 pa,m において市場から持ちかえって所有者が保留するであろう部分を示す。一般に、Qb, pa, Da 及びYの間には、次の関係がある。Qb=Y+Dapa
そして xy=Qb すなわち Qb 点を通る曲線は、(B)の存在量を表わす双曲線であるから、AdAp は、(B)で表わした(A)の価格のxy=Qa
を方程式とする(A)の存在量の双曲線との間にも、同様の関係があるのはもちろんである。五五 故に需要曲線は、量の双曲線のうちに包まれている。またこれらの需要曲線は一般に坐標軸を切り、これらの軸と漸近線をなさないということが出来る。
一般に需要曲線は、需要の軸を切る。なぜなら価格零においてある個人によって需要せられるある商品の量は、一般に有限であるから。例えば燕麦が無償で与えられるとしたら、ある人は十頭、ある人は百頭の馬を飼養するかもしれぬ。しかし彼らは無限数の馬を飼養せぬであろうし、従って無限量の燕麦を需要せぬであろう。ところで価格零における需要の総計は有限量の合計であるから、それ自身も有限量である。
需要曲線は一般に価格の軸を切る。実際価格が無限大に達しなくても充分に高ければ、ある商品がその無限小量をも何人によっても需要せられないようになるであろうと、我々は想像し得る。しかしこの点については絶対的にはいい得ない。(B)がいかなる価格ででも全部供給せられ得て、従って需要曲線 AdAp が Qb を通る双曲線と合致する場合があり得るし、また(B)の一部がいかなる価格ででも供給せられ得て、従って需要曲線 AdAp が Qb を通る双曲線の内側の双曲線と合致する場合があり得る。だから架空の臆説をしないように、需要曲線が坐標軸と存在量の双曲線との間のすべての地位をとり得ると考えておく。
五六 かくて我々は、一つの商品の有効需要と他の商品で表わしたその価格との間の直接的関係を知り、またこの関係の数学的表現を知り得たわけである。
例えば(A)商品についていえば、この関係は幾何学的には、曲線 AdAp により、また代数的には、この曲線の方程式
Da=Fa(pa)
によって表わされる(第五二節)。(B)商品についていえば、この関係は、幾何学的には曲線 BdBp により、代数的には、この曲線の方程式
Db=Fb(pb[#「b」は底本では上付き小文字])
によって表わされる。その上、我々は、ある他の商品と交換に提供せられる一つの商品の有効供給と、後者で表わした前者の価格との間に存する間接的関係の性質を知り得たわけであり、またこの関係の数学的表現を知り得たわけである。
例えば(A)についていえば、この関係は、幾何学的には曲線 BdBp で包まれた一連の矩形により、また代数的には、この曲線の方程式
Oa=Dbpb=Fb(pb)pb
によって表わされる(第五三節)。(B)については、それは幾何学的には、曲線 AdAp に包まれた一連の矩形により、代数的には、方程式
Ob=Dapa=Fa(pa)pa
によって表わされる。ところで、これらの方程式から、各商品の有効供給と他の商品で表わしたこの商品の価格との関係を表わす方程式を導き出すことは容易である。すなわちこれら二つの方程式において、価格 pb を
よって

これらの要素をもって私共は、二商品の交換の一般的問題||二商品(A)、(B)を与えられ、またこれら二商品相互の需要曲線またはこれら曲線の方程式を与えられれば、それぞれの均衡価格はいかに定まるかの問題||を、数学的に解くことが出来る。
五七 幾何学的には、問題は、二つの曲線 AdAp, BdBp の間に、それぞれの底辺(これらは互に逆数である)上に矩形 OdaApa, ODbBpb を作り、これら一方の高さ ODa が他方の面積 ODb × Opb に等しくなるように、また反対にこの他方の矩形の高さ ODa が一方の矩形の面積 ODa × Opa に等しくなるようにすることにある。これら二つの矩形の底辺 Opa, Opb は均衡価格を示す。けだしこれらの価格のそれぞれにおいて、高さ ODa によって表わされる(A)の需要は、面積 ODa×Opa によって表わされる(B)の供給に等しいからである(第四七節)。
ここに用いた「各一方の矩形の高さが他方の矩形の面積に等しくなるように」という表現は、等質を表現したものではない。しかしこの場合にはこの等質を必ずしも必要としない。なぜなら底辺が互に逆数を表わしていることが、これら二曲線の構成に役立った共通な単位 O1 の存在を予想しているから。だがもしこの単位を
五八 代数的には、問題は、二つの方程式
Fa(pa)=Fb(pb)pb, papb=1
における二つの根 pa, pb を求め、または二つの方程式Fa(pa)pa=Fb(pb), papb=1
における二つの根 pa, pb を求めることにある。更にいい換えれば、問題は、Da=Oa
を表わす方程式
Ob=Db
を表わす方程式
五九 なおまた、これらの解法を一つに結合することも出来る。我々は既に曲線
Da=Fa(pa[#「a」は底本では「b」]), Db=Fb(pb)
を知っているが、これらはそれぞれ曲線 AdAp, BdBp である。今曲線
これらの曲線 KLM, NPQ はいかなるものであるか、図に点線で表わされたこれらの曲線の構造の形状を知ることは容易である。
まず曲線 KLM は(A)の供給曲線であって、(B)の需要曲線と混同してはならない。なぜなら(B)の需要曲線の坐標によって作られる矩形の面積は、価格 pb の函数としての(A)の供給を示しているのに反し、(A)の供給曲線の縦坐標の長さは、価格 pa の函数としての(A)の供給を示しているから。
この曲線は、(B)で表わした(A)の価格が無限大であるときすなわち(A)で表わした(B)の価格が無限小であるとき、零の値から出発し、従って価格の軸に漸近線をなす。そしてそれは、原点に近づくに従い、すなわち(B)で表わした(A)の価格が減少するに従い、すなわち(A)で表わした(B)の価格が増加するに従って、上向し、ついに最高点Lに達する。この点の横坐標は、曲線 BdBp に包まれる矩形の面積を最大ならしめる Bm 点の横坐標 Opb,m によって表わされる pb,m すなわち(A)で表わした(B)の価格の逆数、すなわち(B)で表わした(A)の価格を示している。次にこの曲線は、原点に近づくに従い高さを減じ、ついに零となる。これが零となるのは、曲線 BdBp が価格の軸を切る Bp 点の横坐標 OBp によって表わされる(A)で表わした(B)の価格の逆数においてである、すなわち OK で示される(B)で表わした(A)の価格においてである。
同様に曲線 NPQ は(B)の供給曲線であって、(A)の需要曲線と混同してはならない。(A)の需要曲線の坐標によって作られる矩形の面積は、価格 pa の函数としての(B)の供給を示しているのに反し、(B)の供給曲線の縦坐標の長さは、価格 pb の函数としての(B)の供給を示している。
この曲線は、(A)で表わした(B)の価格が無限大であるときすなわち(B)で表わした(A)の価格が無限小であるとき、零の値から出発し、従って価格の軸に漸近線をなす。そしてそれは、原点に近づくに従い、すなわち(A)で表わした(B)の価格が減少するに従い、すなわち(B)で表わした(A)の価格が増大するに従い、上向し、ついに最高点Pに達する。この点の横坐標は、曲線 AdAp に包まれた矩形の面積を最大ならしめる Am 点の横坐標 Opa,m によって表わされる pa,m の逆数すなわち(B)で表わした(A)の価格を示す。次にこの曲線は、原点に近づくに従い、高さを減じ、ついに零となる。これが零となる点は、曲線 AdAp が価格の軸を切る Ap 点の横坐標 OAp によって表わされる(B)で表わした(A)の価格の逆数においてである。すなわち ON によって示される(A)で表わした(B)の価格においてである。
いうまでもなく、曲線 KLM, NPQ の形状は全く曲線 BdBp, AdAp の形状
六〇 だから、もしA点において二曲線 AdAp, KLM が交わるとしたら、この点の右においては曲線 AdAp は曲線 KLM より小であり、左においてはより大であることも明らかである。またB点において二曲線 BdBp, NPQ が交わるとすれば、この点の右においては、曲線 BdBp は曲線 NPQ より小であり、左においてはより大であることも明らかである。
ところで、価格
 は、仮定によって、Da=Oa, Db=Ob ならしめる価格であるから、pa より大なるすべての(B)で表わした(A)の価格においては、すなわち pb より小なるすべての(A)で表わした(B)の価格においては、Oa>Da であり、Db>Ob である。反対に pa より小なるすべての(B)で表わした(A)の価格においては、すなわち pb より大なる(A)で表わした(B)の価格にあっては、Da>Oa であり、同時に Ob>Db である。前の場合には pb の高騰すなわち pa の下降によってしか、均衡価格が現われ得ないし、後の場合には pa の高騰すなわち pb の下落によってしか、均衡価格は現われ得ない。
は、仮定によって、Da=Oa, Db=Ob ならしめる価格であるから、pa より大なるすべての(B)で表わした(A)の価格においては、すなわち pb より小なるすべての(A)で表わした(B)の価格においては、Oa>Da であり、Db>Ob である。反対に pa より小なるすべての(B)で表わした(A)の価格においては、すなわち pb より大なる(A)で表わした(B)の価格にあっては、Da>Oa であり、同時に Ob>Db である。前の場合には pb の高騰すなわち pa の下降によってしか、均衡価格が現われ得ないし、後の場合には pa の高騰すなわち pb の下落によってしか、均衡価格は現われ得ない。そこで、二商品相互の間の交換における有効需要供給の法則(loi de l'offre et de la demande effectives)すなわち均衡価格成立の法則(loi d'
 stablissement d'
stablissement d' quilibre)を、次のように表現することが出来る。||二商品が与えられ、それらについて市場の均衡すなわちそれぞれ一方の商品で表わした他方の価格の静止状態があり得るためには、二商品の各々の有効需要がその有効供給に等しいことを必要とし、またこれだけの条件が充されるだけで充分である。この均等が存在しないとすると、均衡価格に達するためには、有効需要が有効供給より大なる商品の価格が高騰せねばならぬし、有効供給が有効需要より大なる商品が下落せねばならぬ。
quilibre)を、次のように表現することが出来る。||二商品が与えられ、それらについて市場の均衡すなわちそれぞれ一方の商品で表わした他方の価格の静止状態があり得るためには、二商品の各々の有効需要がその有効供給に等しいことを必要とし、またこれだけの条件が充されるだけで充分である。この均等が存在しないとすると、均衡価格に達するためには、有効需要が有効供給より大なる商品の価格が高騰せねばならぬし、有効供給が有効需要より大なる商品が下落せねばならぬ。この法則は、先に取引所の市場の研究のすぐ後で表明しようと試みたものであるが(第四二節)、しかしその厳密な証明が必要であった(第四八節)。
六一 我々は今や、市場における競争の機構がいかなるものであるかを、よく理解し
[#改ページ]
第七章 二商品相互の間に行われる交換の問題の解法の吟味
要目 六二、六三 供給曲線が唯一の極大において連続である場合に論議を局限する。六四 供給曲線は需要曲線と交わらないこともあり得る。この場合価格は成立しない。六五 供給曲線は需要曲線と三点において交わることもあり得る。この場合三つの価格があり得る。六六、六七、六八 この内二つの均衡価格は安定であり、一つの均衡価格は不安定である。六九 二つの需要曲線の内一つが存在量の双曲線と一致する場合。七〇 二つ共一致する場合。
六二 以上述べてきた所を要約すれば、二商品(A)、(B)が与えられ、その有効需要と価格との関係が、方程式
Da=Fa(pa), Db=Fb(pb)
によって表わされるとすると、均衡価格は方程式Dava=Dbvb
によって得られる。そして Da, Db にその値を代入すれば、均衡価格は方程式Fa(pa)va=Fb(pb)vb
によって得られる。だがしかし、pa を求めようとするならば、更に右の方程式を次の[1]の形とすることも出来、また pb を求めようとするならば、それを[2]の形とすることも出来る。
私は、これら二つの形の方程式を、曲線


六三 けれども今は、可能なあらゆる場合についてこの解法を吟味するのではない。あらゆる場合についてこの解法を吟味するのは、多大の時を要し、またここはその機会ではない。ただ示した図に関するような極めて簡単な一般的場合のみを吟味する。第二図においては、私は、曲線 AdAp, BdBp が連続であると考え、かつまた
Da=OAd, pa=0 なる点と
pa=OAp, Da=0 なる点との間に、及び
Db=OBd, pb=0 なる点と
pb=OBp, Db=0 なる点との間に、これら曲線上のそれぞれの坐標によって作られる矩形 Dapa, Dbpb がもち得る極大はそれぞれただ一つであると考えておいた。のみならず第二図については、正の坐標が作る角のうちに含まれる曲線の部分、しかもこの角のうちでも、点 Ad と Ap との間に含まれた曲線の部分と、点 Bd と Bp との間に含まれた曲線の部分とを考察すればよいのであった。もちろんこのことは交換という事実の性質上当然に出てくる。この仮定においては、曲線 KLM, NPQ は連続曲線であり、それらのそれぞれの坐標によって作られる矩形の面積は、ただ一つの極大を示すに過ぎない。だがかく限定せられた場合においても吟味せられるべき興味ある問題がある。pa=OAp, Da=0 なる点との間に、及び
Db=OBd, pb=0 なる点と
六四 私の推論中では、一方 AdAp 及び KLM、他方 BdBp 及び NPQ は、それぞれ唯一点A及びBにおいてしか交わらないと考えられた。けれどもまずこれらの曲線はどこでも交わらない場合もあり得ることを注意すべきである。まことに、もし曲線 BdBp がN点の手前に位する点において価格の軸に達するとすれば、それは曲線 NPQ とは交わらない。かつこの場合には曲線 KLM は Ap 点よりも遠い点において価格の軸を去り、曲線 AdAp には交わらない。従って問題はこの場合には解けない。
このことは驚くに足らない。この場合は、(B)のいずれの所有者も(A)の1に対して(B)の Ap を、すなわち(A)の
六五 次に、曲線の形状を注意して観察すれば、二曲線の間に多数の交点がある場合があり得ることが解る。まことにもし二商品(A)、(B)について、(B)をもってする(A)の需要が曲線 AdAp を示し、(A)をもってする(B)の需要が曲線 Bd'Bp' を示すとすれば、この曲線 Bd'Bp' は曲線 NPQ と三つの点 B, B', B'' において交わるであろう。この場合には、(B)と交換せられる(A)の供給曲線 KLM は、曲線 K'L'M' となるのであって、これは三つの点 A, A', A'' において曲線 AdAp に交わるであろう。A, A', A'' はそれぞれ B, B', B'' 点に対応する。この場合には二商品(A)、(B)の相互の交換の問題に三つの解があり得る。なぜなら曲線 AdAp, Bd'B'p に包まれて互に逆数である底辺をもちかつ高さが互に他方の面積に等しい二つの矩形の三組があり得るからである。だがこれら三つの解は、いずれも同一の価値をもつものであろうか。
六六 三つの組のうち、まず、点 A' と B' の組、及び点 A'' と点 B'' の組を検討すれば、それらは、ただ一つの解しかあり得ない場合における点A及びBの組と同様の状態にあることが解る(第六〇節)。曲線 AdAp は A' 点すなわち二曲線 AdAp,K'L'M'[#「'」は底本では下付き] の交点の右方であるかまたは左方であるかにより、曲線 K'L'M' より小であるかまたは大である。同様に曲線 B'dB'p は、B' 点すなわち二曲線 B'dB'p と NPQ とが交わる点の右方であるかまたは左方であるかにより、曲線 NPQ より小であるかまたは大である。また曲線 AdAp は、 A'' 点の右方であるかまたは左方であるかにより曲線 K'L'M' より小であるかまたは大である。同様にまた曲線 B'dB'p は、B'' 点の右方であるかまたは左方であるかにより、曲線 NPQ[#「NPQ」は底本では「NRQ」] より小であるかまたは大である。
これら二つの場合にあっては、均衡点の彼方において、商品の供給はその需要を超え、価格の下落すなわち均衡点への復帰を生ずる。また均衡点の此方において、商品の需要はその供給を超え、価格の騰貴すなわち均衡点への前進が生ずる。だからこの均衡を、私共は、垂直線上にある重心の上方に
 quilibre stable)である。
quilibre stable)である。六七 点 A, B は同様ではない。A点の右においては曲線 AdAp は曲線 K'L'M' より大であり、左においては小である。同様にB点の右においては、曲線 B'dB'p は曲線 NPQ より大であり、左においてはより小である。だからこの場合には、均衡点の
 quilibre instable)である。
quilibre instable)である。六八 故に実のところ、A', B' の組と A'', B'' の組とがこの問題の二つの解法を成すものであり、A, B の組は、これら二つの解法の各々のそれぞれの領域の分岐点と極限とを示すに過ぎない。pb=μの彼方では、(A)で表わした(B)の価格は、均衡価格 p''b すなわち B'' 点の横坐標に近づいていく。その此方では、価格 p'b すなわち B' 点の横坐標に近づいていく。これと相関的に、
 の此方においては、(B)で表わした(A)の価格は、均衡価格 p''a すなわち A'' の横坐標に近づいていく。この彼方においては、それは、価格 p'a すなわち A' 点の横坐標に近づいていく。
の此方においては、(B)で表わした(A)の価格は、均衡価格 p''a すなわち A'' の横坐標に近づいていく。この彼方においては、それは、価格 p'a すなわち A' 点の横坐標に近づいていく。容易に認め得るように、この事実は、商品の性質により、(B)で表わした(A)の価格が小さいとき需要せられる大なる量の(A)が、(A)で表わした(B)の価格が大なるとき需要せられる小なる量の(B)に等価であり得ると同時に、また(B)で表わした(A)の価格が大なるとき需要せられる小なる量の(A)が、(A)で表わした(B)の価格が小なるとき需要せられる大なる量の(B)に等価となり得る場合に現われる。そこでせりが、(B)で表わした(A)の価格の小なるものと、(A)で表わした(B)の価格の大なるものとをもって始まるか、または(A)で表わした(B)の価格の小なるものと、(B)で表わした(A)の価格の大なるものとをもって始まるかに従い、これら二つの均衡の第一に終るかまたは第二に終ることとなるのである。多数の商品が価値尺度財または貨幣の仲介により互に交換せられる場合にも、なおこの事実が可能であるか否か。私は後にこれを考察しよう。
六九 以上の研究にあっては、需要曲線 AdAp, BdBp, B'dBp' は二つの坐標軸を切ると仮定せられている。けれども需要曲線が存在量の双曲線と一致し、これらの坐標軸に漸近線をなす極端な場合をも研究せねばならぬ。
例えば AdAp が双曲線 Dapa=Qb と一致し、(B)はあらゆる価格においてすべて供給せられるとすると、方程式〔1〕は、

 すなわち pa=∞
すなわち pa=∞そして、方程式〔2〕は、
Qb=Fb(pb)
となる。これは、曲線 BdBp と、ON'=Qb の距離を保って価格の軸に平行に引いた直線 N'P'Q' との交点が πb にあることを示す。七〇 最後に、もし二商品がすべての価格で供給せられるとすれば、同時に


Qava=Qbvb
そして容易に認め得られるように、存在量と交換量とが相等しいのは、二商品の有効需要と有効供給とが相等しいことを表わしている。[#改ページ]
第八章 利用曲線または欲望曲線。商品の利用の最大の法則
要目 七一 部分的需要曲線の出発点を決定する事情。外延利用。七二 傾斜と到達点を決定する事情。強度利用。七三 所有量の影響。七四 利用または欲望の測定単位の仮説。利用曲線または欲望曲線の構成。七五 それらは有効利用及び稀少性を所有量の函数として表示した曲線である。七六 交換は欲望の最大満足の見地から行われる。七七 Bの量 Ob とAの量 da との交換は、交換後においてAの稀少性とBの稀少性との比が価格 pa に等しいときに有利である。七八、七九 この交換は Ob 及び da より小なるかまたは大なる他のすべての二商品の交換よりも有利である。八〇 それ故稀少性の比が価格に等しいときに、欲望の最大満足が生ずる。八一 最大満足の条件から導き出された需要曲線の方程式。八二 無限小による解法。八三、八四 欲望曲線が不連続の場合。
七一 ここまでは、交換の事実の性質について研究をしてきたが、この研究により、またこの事実の原因の研究も可能となる。実際もし価格が需要の曲線から数学的に出てくるとすれば、需要曲線の成立及び変化の第一原因と条件とは、また価格の成立及び変化の第一原因と条件であるべきである。
故に今、部分的需要曲線例えば(B)の所有者(1)の(A)の対するせり上げの傾向を幾何学的に示す所の ad,1ap,1(第一図)(第五一節)に立返り、まずこの曲線が需要の軸を離れてゆく点 ad,1 の位置を決定する事情を考察してみる。長さ Oad,1 は(B)の所有者(1)が(A)を、この価格が零であるときに、有効に需要する量すなわちこの商品が無償で与えられるときにこの人によって消費せられる量を示す。この量は一般に何によって決定せられるか。それは、商品の利用の一種であって私がここで外延利用(utilit
 d'extension または utilit
d'extension または utilit extensive)と呼ぶ所のものによって決定せられる。私がここで外延利用という名辞を用いたのは、この利用を有する種類の冨によって充足せられる欲望の普遍性と数量とが、この欲望を感ずる人々の多少及び感ずる強度の大小によって決定せられるからである。一言でいえば、獲得のために何らの犠牲を提供する必要が無いとすれば、その場合にこの商品が多量に消費せられるかまたは少量だけしか消費せられないかが、外延利用である。ところで(A)の外延利用は(A)の需要曲線にしか影響を与えないという意味で、また同様に(B)の外延利用は(B)の需要曲線にしか影響を与えないという意味で、この第一の事情は簡単であり、絶対的である。かつ外延利用は価格零において需要せられる量であるから計量出来る大いさであるという意味において、この第一の事情は計量し得られるものである。
extensive)と呼ぶ所のものによって決定せられる。私がここで外延利用という名辞を用いたのは、この利用を有する種類の冨によって充足せられる欲望の普遍性と数量とが、この欲望を感ずる人々の多少及び感ずる強度の大小によって決定せられるからである。一言でいえば、獲得のために何らの犠牲を提供する必要が無いとすれば、その場合にこの商品が多量に消費せられるかまたは少量だけしか消費せられないかが、外延利用である。ところで(A)の外延利用は(A)の需要曲線にしか影響を与えないという意味で、また同様に(B)の外延利用は(B)の需要曲線にしか影響を与えないという意味で、この第一の事情は簡単であり、絶対的である。かつ外延利用は価格零において需要せられる量であるから計量出来る大いさであるという意味において、この第一の事情は計量し得られるものである。七二 だが外延利用は利用のすべてではない。それはこの一因子に過ぎない。このほかに、今曲線 ad,1ap,1 の傾斜を決定する事情と、この曲線が価格の軸に達する点 ap,1 の位置を決定する事情とを研究すれば、直ちに明らかになってくる他の利用がある。ところで曲線の傾斜は二つの量すなわち価格の増大とこの増大によって惹き起される需要の減少との比に他ならない。この比は一般に何に依存するか。それは私が強度利用(utilit
 d'intensit
d'intensit または utilit
または utilit intensive)と名附ける利用の一種に依存するのである。この利用を強度利用と名附ける理由は、この利用を有する富によって満足される欲望が、価格が高いのにもかかわらず、多くの人々の間に存するかまたは少数の人々の間に存するか、また各人においては強く存在するかまたは弱く存在するかによって、この利用が強いものであるかまたは弱いものであるかが明らかになるからである。一言でいえば、この商品を獲得するために払う犠牲の程度が、商品の消費量の大小に影響するのは、強度利用の結果である。この事情は、外延利用と異り、(A)の需要曲線の傾斜が、(B)の需要曲線と同じく、(A)の強度利用及び(B)の強度利用の双方によって決定せられるという意味において複雑であり、相対的である。だから需要曲線の傾斜を、需要の減少の価格の増大に対する比の極限〔訳者註、需要を価格につき微分した微分係数〕||これは数学的に決定することの出来る事情であるが||と定義すれば、それは二商品の利用の強度の複雑な関係に他ならないということになる。
intensive)と名附ける利用の一種に依存するのである。この利用を強度利用と名附ける理由は、この利用を有する富によって満足される欲望が、価格が高いのにもかかわらず、多くの人々の間に存するかまたは少数の人々の間に存するか、また各人においては強く存在するかまたは弱く存在するかによって、この利用が強いものであるかまたは弱いものであるかが明らかになるからである。一言でいえば、この商品を獲得するために払う犠牲の程度が、商品の消費量の大小に影響するのは、強度利用の結果である。この事情は、外延利用と異り、(A)の需要曲線の傾斜が、(B)の需要曲線と同じく、(A)の強度利用及び(B)の強度利用の双方によって決定せられるという意味において複雑であり、相対的である。だから需要曲線の傾斜を、需要の減少の価格の増大に対する比の極限〔訳者註、需要を価格につき微分した微分係数〕||これは数学的に決定することの出来る事情であるが||と定義すれば、それは二商品の利用の強度の複雑な関係に他ならないということになる。七三 なお(A)の需要曲線 ad,1ap,1 の傾斜に影響を有する他の事情がある。それは(B)商品の所有者(1)の手中に存在する(B)の量 qb である。一般に部分的需要の曲線が部分的存在量の双曲線より小さいのは、総需要の曲線が全部量の双曲線より小さい如くである。故に部分量の双曲線が原点に近づきつつ、または原点を離れつつ変化するかに従って、部分的需要の曲線もそれと同様に変化し、あたかも強度利用の変化の結果として現われるように見える。これら二つの場合におけるこの必然的関係を、図は忠実に示している。
七四 この分析は不完全でありながら、一見これ以上にこの分析を一層深く押し進めることは不可能のように見える。なぜなら絶対的強度利用は、外延利用及び所有量と異り、時間にもまた空間にも、直接のかつ計量し得る関係を有しないため、測定し得られないという事実があるからである。けれどもこの困難は越え得ないものではない。今私は、右のような関係が存在すると仮定し、外延利用、強度利用、及び所有量がそれぞれ価格に及ぼす影響を正確に数学的に説明しようと思う。

故に私は、欲望の強度すなわち強度利用を計量し得る所の、かつ同種類の富のすべての単位にのみならずあらゆる種類の富のすべての単位に共通な尺度の存在を仮定する。今縦軸 Oq 横軸 Or を二つの坐標軸であるとする(第三図)。縦軸 Oq 上に、原点 O から順次に長さ Oq', q'q'', q''q''', ······をとり、これらをもって、(B)の所有者(1)が自ら現にこれらを所有するとすれば、ある時間のうちに順次に消費していくであろう所の単位数を表わさしめる。かつ外延利用及び強度利用は、この時間中、各交換者に対し一定であると仮定する。これによって、利用という表現のうちに、私は時間を暗黙のうちにだけ示しておくに止めることが出来る。もし反対に、利用が時間の函数として変化するものであると仮定すると、問題の中に時間が明示的に現われてこなければならぬ。この場合には経済静態を離れて、動態(dynamique)に入ることになる。
ところでこれら順次の単位は、所有者(1)に対し、充足要求の最も強い欲望を充すべき第一の単位から、消費すれば飽満を感ぜしめるような最終の単位まで、次第に強さを減じていく強度利用をもつものであって、私共はこの減少を数学で表現しなければならぬ。もし商品(B)が、例えば家具、衣服のように、自然に単位ずつ消費せられるとすれば、横軸 Or の上、及び点 q', q'' ······等を通って横軸に平行な線の上に、原点及びこれらの q', q'' から長さ Oβr,1, q'r'', q''r''' をとり、これらでそれぞれ、これらが表わす単位の強度利用を表わさしめる。また矩形 Oq'R'βr,1, q'q''R''r'', q''q'''R'''r''' を作る。かようにして、曲線 βr,1R'r''R''r'''R''' を得る。この曲線は連続ではない。反対にもし(B)が、例えば食料品のように、微分小量ずつ消費し得られるとすると、利用の強度は、一単位から次の単位へと、減少するのみでなく、各単位の第一部分から最後の部分まで順次に減少し、不連続曲線 βr,1R'r''R''r'''R''' は連続曲線 βr,1r''r''' ··· βq,1 に変化する。同様にして、(A)について曲線 α[#「α」は底本では「a」]r,1α[#「α」は底本では「a」]q,1 を得ることが出来る。かつ曲線が不連続な場合と同じく、連続な場合にも、利用の強度は第一単位またはこの単位の第一部分の強度から、消費せられる最後の単位またはこの単位の最後の部分の強度まで、逓減する事実が認められる。
長さ Oβq,1, Oαq,1 は、所有者(1)に対し商品(B)及び(A)がもつ外延利用すなわち所有者(1)が商品(B)及び(A)についてもつ欲望の外延を示す。面積 Oβq,1βr,1,Oαq,1αr,1 は、商品(B)及び(A)が同じ所有者(1)に対してもつ可能的利用(utilit
 s virtuelles)すなわち所有者(1)が商品(B)及び(A)についてもつ欲望の外延及び強度の合計を示す。故に曲線 αr,1αq,1,βr,1βq,1 は、所有者(1)につき、(B)及び(A)の利用曲線(courbes d'utilit
s virtuelles)すなわち所有者(1)が商品(B)及び(A)についてもつ欲望の外延及び強度の合計を示す。故に曲線 αr,1αq,1,βr,1βq,1 は、所有者(1)につき、(B)及び(A)の利用曲線(courbes d'utilit s)または欲望曲線(courbes de besoins)を示す。だがそれだけではない。これらの曲線はまた二面の性質をもっている。
s)または欲望曲線(courbes de besoins)を示す。だがそれだけではない。これらの曲線はまた二面の性質をもっている。七五 ある商品の消費せられた量により、外延においてまた強度において、充足せられた欲望の合計を有効利用(utilit
 effective)と呼べば、曲線 βr,1βq,1 は、(B)の消費量の函数としてのこの人に対する有効利用の曲線を示す。例えば長さ Oqb によって表わされる消費量 qb のこの人に対する有効利用は面積 Oqbρβr,1 によって表わされる。そして商品の消費せられた量によって充される最後の欲望の強度を稀少性(raret
effective)と呼べば、曲線 βr,1βq,1 は、(B)の消費量の函数としてのこの人に対する有効利用の曲線を示す。例えば長さ Oqb によって表わされる消費量 qb のこの人に対する有効利用は面積 Oqbρβr,1 によって表わされる。そして商品の消費せられた量によって充される最後の欲望の強度を稀少性(raret )と呼べば、曲線 βr,1βq,1 は(B)の消費量の函数としてのこの所有者に対する稀少性の曲線(courbe de raret
)と呼べば、曲線 βr,1βq,1 は(B)の消費量の函数としてのこの所有者に対する稀少性の曲線(courbe de raret )となるであろう。だから長さ Oqb によって表わされる消費量 qb の稀少性は、長さ
)となるであろう。だから長さ Oqb によって表わされる消費量 qb の稀少性は、長さqbρ=Oρb
によって表わされる ρb である。同様に曲線 ar,1aq,1 は(A)の消費量の函数としての有効利用の曲線または稀少性曲線。それ故に横軸及び縦軸を、それぞれ稀少性の軸(axe des raret s)、量の軸(axe des quantit
s)、量の軸(axe des quantit s)と呼ぶことが出来るわけである。繰り返していうが、稀少性は所有量が減少するときに増加するものであり、その逆もまた真であることを、我々は認めねばならぬ。
s)と呼ぶことが出来るわけである。繰り返していうが、稀少性は所有量が減少するときに増加するものであり、その逆もまた真であることを、我々は認めねばならぬ。代数的には、有効利用は、消費量の函数として、方程式
u=Φa,1(q),u=Φb,1(q)
によって与えられ、稀少性はその微分係数 Φ'a,1(q), Φ'b,1(q) によって与えられる。もしまた稀少性を、消費量の函数として、方程式r=φa,1(q),r=φb,1(q)
によって表わせば、有効利用は 0 より q までの定積分

r=φa,1(q)
によって表わされ、この同じ所有者に対する(B)の外延利用及び強度利用は、幾何学的には、連続曲線 βr,1βq,1 により、代数的には、この曲線の方程式r=φb,1(q)
によって表わされる。そして長さ Oqb によって表わされる量 qb は、この所有者が所有する(B)の量であるが、ある価格が現われたとき、この所有者が(A)に対してもつ需要はいかなるものであるか。それを正確にし得るか否かを見ようと思う。欲望曲線を作った方法並びにこれらの曲線を作るとき認められたこれらの曲線の性質から明らかであるように、この人が(B)の qb 量を所有し、そのすべてを消費するとすれば、面積 Oqbρβr,1 によって表わされる欲望の合計量が満足せられる。だがこの人は、一般に、このすべてを消費しないであろう。なぜなら一般に、この人は自分が所有するこの商品のただ一部分のみを消費し、他の部分を、市場の価格で、(A)のある量と交換して、より多い合計量の欲望を満足し得るからである。例えば(B)で表わした(A)の価格が pa であるとき、Oy で表わされる y 単位数の(B)のみを残し、yqb によって表わされる部分すなわち
ob=qb[#「qb」は底本では「qq」]-y
を、Oda によって表わされる da 単位数の(A)と交換すれば、この個人は、二つの面積 Oyββr,1 及び Odaααr,1 によって表わされる欲望の合計を満足することが出来、この量は先の合計量より大となることがあり得る。交換を行うに当ってこの個人は出来得る限り多くの欲望の合計量を満足しようとすると仮定してみると、pa が与えられているのであるから、da は、二つの面積 Oyββr,1,Odaααr,1 の合計が最大となるような条件によって決定せられることは明らかである。ところでこの条件は、量 da 及び y によって満足せられる欲望の最後のもののそれぞれの強さ ra,1 と rb,1 との比すなわち交換後におけるそれぞれの稀少性の比が pa に等しいということである。七七 いまこの条件が充されたと仮定し、
ob=qb-y=dapa
ra,1=parb,1
であるとすると、この式から pa を消去し、ra,1=parb,1
dara,1=obrb,1
を得べく、da, ob, ra,1, rb,1 を、これらを表わす長さ Oda, qby, daα, yβ で置き替えればOda×daα=qby×yβ
それ故に二つの矩形 Odaαra,1, yqbRβ の面積は相等しい。しかるに曲線 αr,1[#「,1」は底本では「,1,」]αq,1, βr,1βq,1 の性質によって、一方において面積 Odaααr,1>Oda×daα
であり、他方qby×yβ> 面積 yqbρβ
である。故に面積 Odaααr,1> 面積 yqbρβ
このようにして、(B)の ob 量と(A)の da 量との交換は我が(B)の所有者にとって有利である。なぜならこれによって得られる満足を表わす面積は、この交換を七八 この証明をなすため、(B)の ob 量と(A)の da 量との交換の全過程が、相等しくてかつ順次に系列をなすs個の部分的交換から成立していると仮定する。しからば交換方程式

Od'a を、Oの点より上方に向って、Oda から切りとった長さとし、qby' を、qb より下方に向って qb[#「b」は底本では上付き小文字]y から切りとった長さとし、かつこれらの長さを、それぞれ第一の部分的交換において交換される(A)の
ra>parb
である。故に前の方程式により、
Od'a×d'aα'>qby'×y'β'
となる。だが欲望曲線の性質によって、一方においては、面積 Od'aα'αr,1>Od'a×d'[#「d'」は底本では「d」]aα'
であり、他方、qb[#「b」は底本では上付き小文字]y'×y'β'> 面積 y'qbρβ'
である。故に面積 Od'aα'αr,1> 面積 y'qbρβ'
である。だから(B)の更に、dad''a を、da 点から下方に向って daO から切りとった長さとし、yy'' をy点から上方に向い yqb から切りとった長さとし、これらの長さは、それぞれ最後の部分的交換において交換せられた(A)の量
ra,1=parb,1
であり、交換方程式により
dad''a×daα=yy''×yβ
しかるに欲望曲線の性質により、一方において面積 d''adaαα''>dad''a×daα
であり、他方yy''×yβ> 面積 yy''β''β
このようにして、(B)の七九 同様にして、ob より大なる(B)の量を供給しないであろうことも、また da より大なる(A)の量を需要しないであろうことも、証明することが出来よう。なぜならこの限度を超える部分的交換は、いかに小なる部分的交換であっても、たとい想像し得る限り小さい最初の部分的交換であっても、いずれも不利益であり、また各部分的交換はますます不利益となるからである。そしてこの証明は先の証明と全く同様である。まことに交換の限度すなわち(A)の稀少性と(B)の稀少性との比が価格 pa に相等しくなった点を越えて更に、(A)のある量と(B)のある量とを交換し、(A)の稀少性を減少し続け、(B)の稀少性を増加し続ければ、ra
rb,1=pbra,1
すなわち ra,1=parb,1に達するまで、(A)のある量と(B)のある量とを交換すれば、満足の最大に近づくことは、確かである。
八〇 故に(B)によって表わした(A)の価格 pa において、(B)の所有者(1)が供給するであろう(B)の量と、需要するであろう(A)の量とが、
ra,1=parb,1
の関係をもっているとすれば、これらそれぞれの量 ob と da とは、この価格において供給せられるべき量に等しく、これらより少くもなければ、多くもない。一般に、市場において二商品が与えられているとすると、欲望満足の最大すなわち有効利用の最大は、各所有者にとり、充足せられた最後の各満足の強度の比すなわち稀少性の比が、価格に等しくなったときに現われる。この均等が達せられない限り、交換者は、稀少性が自らの価格と他方の商品の稀少性との積より小さい商品を売り、稀少性が、自らの価格と右の商品の稀少性との積より大なる商品を買うのが、有利である。
だから、交換者は、二商品のうち、自分が所有する一商品の全量を供給するのが、利益であることもあり得べく、また相手の商品を全く需要せぬのが利益であることもあり得るであろう。この点については、後に説明しよう。
八一 方程式
ra,1=parb,1
の中の ra,1 及び rb,1 に、それらの値を置き換えれば、この方程式はφa,1(da)=paφb,1(y)=paφb,1(qb-ob)
=paφb,1(qb-dapa)
となる。この方程式は、pa の函数としての da を与える。何となれば、この方程式がこれら二つの変数の第二〔訳者註、da〕に関して解かれているとすれば、この方程式は=paφb,1(qb-dapa)
da=fa,1(pa)
という形をとるからである。これは、所有者(1)が(B)で(A)を需要する場合の需要曲線 ad,1ap,1 の方程式を、まさしく表わしている。故に、方程式r=φa,1(q) 及び r=φb,1(q)
が数学的に確定し得られれば、前の方程式もまた数学的に確定する。ただ右に記した方程式が数学的には確定していないために、方程式da=fa,1(pa)
は経験的に過ぎないものとなっている。かくて、問題||二商品(A)、(B)と各交換者に対するこれら二商品の利用曲線すなわち欲望曲線、またはこれら曲線の方程式、及びこれら商品の交換者の各々によって所有せられる量を与えて、需要曲線を決定する問題||は解けるのである。
八二 以上の解法の方式を、既に用いた微分法の記号によって表わすことは、無意義ではあるまい。
(B)で表わした(A)の価格が pa であるとき、需要せられるべき(A)の量を da とし、供給せられるべき(B)の量を ob=dapa であるとし、従って保留せられるべき(B)の量は qb-ob であるとする。そして qb は、所有者(1)が所有する(B)の量であるから、
[1] dapa+(qb-ob)=qb
また u=Φa,1(q), u=Φb,1(q) をそれぞれ(A)及び(B)が消費量の函数としてこの人に対してもつ有効利用を表わす式であるとし、従ってΦa,1(da)+Φb,1(qb-ob)
は、最大ならしめるべき有効利用の合計であるとする。函数Φの微分係数は本質的に逓減するから、我が交換者の求める最大利用は、二商品の各消費量によって生ずる利用の微分増加量の代数和が零であるときに得られる。なぜならこれらの微分増加量が互に相等しくなく、かつ互に正負相反しているとすれば、微分増加量のより強い商品をより多く需要して、微分増加量のより弱い商品をより少く需要し、または微分増加量のより弱い商品をより多く供給し、微分増加量のより強いものをより少く供給するのが利益であるからである。故に欲望の最大満足を与える条件は、次の方程式によって表わされる。Φ'a,1(da)dda+Φ'b,1(qb-ob)d(qb-ob)=0
ところで一方において消費量の函数としての有効利用の函数の導函数は、稀少性に他ならないし、他方において方程式[1]から生ずる方程式padda+d(qb-ob)=0
により、二商品のそれぞれの消費量の微分と二商品のそれぞれの他方で表わしたそれぞれの価格との積の代数和は零である。故に
φa,1(da)=paφb,1(qb-dapa)
私は微分法に通暁しない読者のためにこれを説明した。しかしその他の読者は次のようにして直ちに理解せられるであろう。次の二式の一方または他方を da について微分せよ。Φa,1(da)+Φb,1(qb-dapa)

そしてその導函数を0と置けば、
φa,1(da)-paφb,1(qb-dapa)=0
すなわちφa,1(da)=paφb,1(qb-dapa)
となる。そしてこの方程式の根は極大を示し、極小を示さない。けだし、函数 Φ'a,1(q) すなわち φa,1(q), Φ'b,1(q) すなわち φb,1(q) は本質的に減少函数であるから、第二次導函数φ'a,1(da)+p2aφ'b,1(qb-dapa)
は必然的に負であるからである。八三 右に与えた私の証明は、欲望曲線の連続を前提とする。だが我々は、欲望曲線が不連続である場合をも研究せねばならぬ。厳密にいえば、これらの場合には、(一)連続曲線をもつ商品と不連続曲線をもつ商品との交換、(二)不連続曲線をもつ商品と連続曲線をもつ商品との交換、(三)不連続曲線をもつ商品と、同じく不連続曲線をもつ商品との交換の三箇の場合があり得よう。けれども、後に明らかにするように、我々はすべての商品の価値をその価値と関係せしめそしてすべての商品を購い得る商品、従って連続的な欲望曲線をもち得るしもたねばならぬ所の一つの商品を選ぶのであるから、第一の場合だけを研究すればよい。
常例により、(B)の所有者(1)に対する(B)の利用曲線を βr,1βq,1(第三図)とし、この人が所有する(B)の量を qb とする。そして点 a 及び a''' を通る階段形の曲線を、この交換者に対する(A)の利用曲線であるとする。(A)は単位ずつによってしか買い得られないのであるから、そして pa は(B)で表わした(A)の価格であるから、(B)は pa に等しい量によってしか売られない。もし長さ dad''a 及び dad'''a がそれぞれ(A)の買われた最後の単位と買われない最初の単位とを表わし、また長さ yy'' 及び yy''' がそれぞれ(B)の売られた最後の量と売られない最初の量とを表わすものとすれば、交換者が最大満足を得るときには、次の二つの不等式が成り立つ。
面積 yy''β''βaa
面積 yy'''β'''β>d'''aa'''
今 m'' と m''' とで、それぞれ yβ と y''β'' との中間の長さ及び yβ と y'''β''' との中間の長さを表わすこととすれば、これらは、それぞれ(B)の売られた最後の量の利用の平均強度及び売られない最初の量の利用の平均強度を示す。これらに面積 yy'''β'''β>d'''aa'''
yy''=yy'''=pa
を乗ずれば、それぞれ yy''β''β 及び yy'''β'''β に等しい二つの面積が得られる。そこで相合して(A)の需要すなわち da を決定する二つの不等式を次の形に立てることが出来る。daa=pam''+ε''
d'''aa'''=pam'''-ε'''
これら二つの方程式から、容易に次の結果を導き出すことが出来る。d'''aa'''=pam'''-ε'''

 ははなはだ小さい量である。故に容易に
ははなはだ小さい量である。故に容易に
よって、連続的欲望曲線をもつ商品と不連続的欲望曲線をもつ商品との交換の場合において、最大満足が現われるときには、買われた商品の充された最後の欲望の強度と充されない最初の欲望の強度との平均の、売られたる商品の充された最後の欲望の強度に対する比は、価格にほぼ等しい。
私はほぼ等しいとあえていう。なぜなら(B)で表わした(A)の価格と、(B)の充された最後の欲望の強度との積 pa×yβ は、(A)の充された最後の欲望の強さと充されない最初の欲望の強さの平均に等しくないことがあり得るのみでなく、また、これら二つの量各々より大であることも、小であることもあり得るからである。実際、必然的に
面積 yy''β''βa×yβ
であり、daa> 面積 yy''β''β
であるけれども、必然的にはdaa>pa×yβ
ではない。そしてもし反対にdaaa×yβ
であるとすると、daa 及びこの daa より小さい d'''aa''' は、いずれも pa×yβ より小である。同様に、必然的に、面積 yy'''β'''β>pa×yβ
であり、d'''aa'''< 面積 yy'''β'''β
である。しかし必然的には、d'''aa'''a×yβ
ではない。そしてもしd'''aa'''>pa×yβ
であるとすると、d'''aa''' 及びこの d'''aa''' より大なる daa は、いずれも pa×yβ より大である。八四 再び二つの不等式
面積 yy''β''βaa
面積 yy'''β'''β>d'''aa'''
を見よう。pa が減少すると、これら二つの不等式の最初の項は共に減少する。これによって、第一式の不等関係には変化は生じない。しかし第二式の不等関係が反対となり、da が少くとも一単位だけ増加する時が来る。pa が増加すると、二つの方程式の初項は増加する。これによって、第二式の不等関係は変化しない。しかし第一式の不等関係が反対となり、da が少くとも一単位だけ減少する時が来る。故に(A)の需要曲線は逓減しかつ不連続である。面積 yy'''β'''β>d'''aa'''
解析的には、(B)で表わした(A)の任意の価格 pa が叫ばれるとき、(B)の所有者は、欲望強度 r1, r2 ······を充す所の(A)の一、二単位を需要し、この同じ r1, r2 ······量で計量せられた(A)の有効利用を得れば、保留せられる(B)の量は、qb-pa, qb-2pa ······となり、定積分


[#改ページ]
第九章 需要曲線論。二商品間における交換の問題の数学的解法の一般的方式
要目 八五 価格零における需要。それは外延利用に等しい。八六 (A)の需要が零の場合の価格。八七 (B)の供給が所有量に等しい場合の価格。八八 供給が所有量に等しい条件、所有量の双曲線と需要曲線とが交わること。八九 双曲線は交点の間では需要曲線となる。九〇 所有量の減少。九一 増加。九二 一般の場合は二商品の所有者の場合である。部分的有効需要の二つの方程式または曲線。九三、九四、九五 各商品の需要方程式、または曲線は同じ商品の供給を価格の函数として表わす式または曲線でもある。九六 二商品間の交換の場合におけるせり上げの傾向を表わす方程式の一般体系。九七、九八 方程式の解法。
八五 部分的需要の方程式
da=fa,1(pa)
は、φa,1(da)=paφb,1(qb-dapa)
を da に関して解いたと仮定した方程式に他ならないから、我々は、部分的需要の方程式を、この後の形において論究することが出来る。まず、pa[#「pa」は底本では「ra」]=0 とすれば、この方程式は
φa,1(da)=0

 の満足を得られるのに反し、この最後の部分を価格 pa で(A)の
の満足を得られるのに反し、この最後の部分を価格 pa で(A)の

 だけの満足しか得られないが、これを価格 pa で(A)の
だけの満足しか得られないが、これを価格 pa で(A)の
 は減少する。qb=0 となるときは、ρb=βr,1 であって、比
は減少する。qb=0 となるときは、ρb=βr,1 であって、比 は
は に一致する。そのときには、需要曲線 ad,1ap,1 は、坐標軸の一部 ad,1Oπ となる。
に一致する。そのときには、需要曲線 ad,1ap,1 は、坐標軸の一部 ad,1Oπ となる。





 及び α>1 の仮定。裁定(B、A、C)、(A、C、B)、(C、B、A)。pa,b の下落。pb,a の下落。pc,a の騰貴。一一五 α>1、逆の操作と結果。一般均衡方程式。一一六 他のすべての商品を反対給付とする各商品の需要と供給の均等の方程式を、他の商品の各々を反対給付とする各商品の需要と供給の均等の方程式に置き換えること。
及び α>1 の仮定。裁定(B、A、C)、(A、C、B)、(C、B、A)。pa,b の下落。pb,a の下落。pc,a の騰貴。一一五 α>1、逆の操作と結果。一般均衡方程式。一一六 他のすべての商品を反対給付とする各商品の需要と供給の均等の方程式を、他の商品の各々を反対給付とする各商品の需要と供給の均等の方程式に置き換えること。
 個の特別の市場に分たれると、想像する。しからば“互に逆数の価格 pa,b, pb,a で行われる(A)と(B)、(B)と(A)との交換”、“互に逆数の価格 pa,c, pc,a で行われる(A)と(C)、(C)と(A)との交換”、“互に逆数の価格 pb,c, pc,b で行われる(B)と(C)、(C)と(B)との交換”、があるわけである。これだけを前提とし、もし、(B)及び(C)を欲する(A)の各所有者が右の第一及び第二の特別市場で、この(A)を(B)及び(C)と交換するに止まるとすれば、またもし、(A)及び(C)を欲する(B)の各所有者が右の第一及び第三の特別市場で、この(B)を(A)及び(C)と交換するに止まるとすれば、またもし(A)及び(B)を欲する(C)の各所有者が第二及び第三の特別市場で、この(C)を(A)及び(B)と交換するに止まるとすれば、均衡はこれらの状態の下において保たれる。だが容易に了解し得るように、(A)の所有者も、(B)の所有者も、(C)の所有者も、この交換の方法を採用しないであろう。彼らはいずれも、自分に最も有利であろう所の方法で交換を行うであろう。
個の特別の市場に分たれると、想像する。しからば“互に逆数の価格 pa,b, pb,a で行われる(A)と(B)、(B)と(A)との交換”、“互に逆数の価格 pa,c, pc,a で行われる(A)と(C)、(C)と(A)との交換”、“互に逆数の価格 pb,c, pc,b で行われる(B)と(C)、(C)と(B)との交換”、があるわけである。これだけを前提とし、もし、(B)及び(C)を欲する(A)の各所有者が右の第一及び第二の特別市場で、この(A)を(B)及び(C)と交換するに止まるとすれば、またもし、(A)及び(C)を欲する(B)の各所有者が右の第一及び第三の特別市場で、この(B)を(A)及び(C)と交換するに止まるとすれば、またもし(A)及び(B)を欲する(C)の各所有者が第二及び第三の特別市場で、この(C)を(A)及び(B)と交換するに止まるとすれば、均衡はこれらの状態の下において保たれる。だが容易に了解し得るように、(A)の所有者も、(B)の所有者も、(C)の所有者も、この交換の方法を採用しないであろう。彼らはいずれも、自分に最も有利であろう所の方法で交換を行うであろう。

 であるときには、(B)の
であるときには、(B)の が得られるからであり、商品(A、C)の市場において、(A)で表わした(C)の価格が
が得られるからであり、商品(A、C)の市場において、(A)で表わした(C)の価格が であるときは、(A)の
であるときは、(A)の であるという結果が出てくる。なぜなら、商品(A、C)の市場において、(A)で表わした(C)の価格が
であるという結果が出てくる。なぜなら、商品(A、C)の市場において、(A)で表わした(C)の価格が が得られ、商品(B、C)の市場において、(C)で表わした(B)の価格が
が得られ、商品(B、C)の市場において、(C)で表わした(B)の価格が であるときには、(C)の
であるときには、(C)の が得られるからである。
が得られるからである。 である。なぜなら、商品(B、C)の市場において、(C)で表わした(B)の価格が
である。なぜなら、商品(B、C)の市場において、(C)で表わした(B)の価格が が得られ、商品(A、B)の市場において、(B)で表わした(A)の価格が
が得られ、商品(A、B)の市場において、(B)で表わした(A)の価格が が得られるからである。
が得られるからである。
 であるという結果が出てくる。なぜなら、商品(A、B)の市場において(B)で表わした(A)の価格が
であるという結果が出てくる。なぜなら、商品(A、B)の市場において(B)で表わした(A)の価格が が得られるからである。
が得られるからである。 であるという結果が出てくる。なぜなら、商品(A、C)の市場で、(A)で表わした(C)の価格が6であるときは、(A)の 1.50 で、(C)の
であるという結果が出てくる。なぜなら、商品(A、C)の市場で、(A)で表わした(C)の価格が6であるときは、(A)の 1.50 で、(C)の が得られ、商品(B、C)の市場において、(C)で表わした(B)の価格が
が得られ、商品(B、C)の市場において、(C)で表わした(B)の価格が が得られるからである。
が得られるからである。 であるという結果が出てくる。なぜなら、商品(B、C)の市場において、(C)で表わした(B)の価格が
であるという結果が出てくる。なぜなら、商品(B、C)の市場において、(C)で表わした(B)の価格が が得られ、商品(A、B)の市場においては、(B)で表わした(A)の価格が
が得られ、商品(A、B)の市場においては、(B)で表わした(A)の価格が が得られるからである。
が得られるからである。 である場合には、市場の均衡は決定的すなわち一般的ではない。だから裁定が行われ、その結果 pc,b は下落し、pc,a は騰貴し、pb,a は下落する。また同時に解るように、
である場合には、市場の均衡は決定的すなわち一般的ではない。だから裁定が行われ、その結果 pc,b は下落し、pc,a は騰貴し、pb,a は下落する。また同時に解るように、 である場合には、市場において裁定が行われ、その結果 pc,b は騰貴し、pc,a は下落し、pb,a は騰貴する。実際この場合には α<1 とすれば、
である場合には、市場において裁定が行われ、その結果 pc,b は騰貴し、pc,a は下落し、pb,a は騰貴する。実際この場合には α<1 とすれば、


















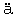 tze der Volkswirtshaftslehre)を公にした。これは、交換の新理論の基礎が、他と独立にかつ独創的な形で説かれた第三の著作であって、私の著作に先行している。メンガーも、私共のように、交換理論を引き出す目的をもって、消費量の増加と共に欲望は逓減するとの法則を立てて、利用理論を説いている。氏は演繹的方法を用いたが、数学的方法を用いることに反対している。しかし、氏は、利用や需要を表わすのに、函数や曲線を用いてはいないが、少くとも算術的表を用いている。この事情により、ゴッセンとジェヴォンスを数行のうちに批評したように、メンガーの理論をも簡単に批評し尽すことは出来ない。私はただ、氏とウィーザーやベェーム=バウェルクのように氏に追従した著作者達とが、ただ本質上数学的な問題に数学的方法と用語を率直に用いることを拒否したのは、貴重にしてかつ欠くべからざる手段を抛棄したものであるといいたい。しかしここで附言しておくが、これらの著者達は、不完全な方法と用語とを用いたとはいえ、交換問題の深い研究を遂げた。少くとも確かに、稀少性の理論すなわち彼らのいわゆる限界利用の理論に経済学者の注意を強く促すのに成功している。今やこの理論は経済学の中に現われて、最も光輝ある未来を予想せられている。私は、この理論から、価値尺度財で表わした商品の価格決定の抽象的理論を導き出した。私は、(一)生産物の価格と土地収入、人的収入、動産収入の同時的決定の理論、(二)純収入率の決定の理論、土地資本、人的資本、動産資本の価格決定の理論、(三)貨幣で表わした価格決定の理論を導き出そうと思う。これらの理論はいずれも抽象的ではあるが、互に関連しているから、組織的な綜合をすれば、現実の説明となり得るであろう(三)。
tze der Volkswirtshaftslehre)を公にした。これは、交換の新理論の基礎が、他と独立にかつ独創的な形で説かれた第三の著作であって、私の著作に先行している。メンガーも、私共のように、交換理論を引き出す目的をもって、消費量の増加と共に欲望は逓減するとの法則を立てて、利用理論を説いている。氏は演繹的方法を用いたが、数学的方法を用いることに反対している。しかし、氏は、利用や需要を表わすのに、函数や曲線を用いてはいないが、少くとも算術的表を用いている。この事情により、ゴッセンとジェヴォンスを数行のうちに批評したように、メンガーの理論をも簡単に批評し尽すことは出来ない。私はただ、氏とウィーザーやベェーム=バウェルクのように氏に追従した著作者達とが、ただ本質上数学的な問題に数学的方法と用語を率直に用いることを拒否したのは、貴重にしてかつ欠くべからざる手段を抛棄したものであるといいたい。しかしここで附言しておくが、これらの著者達は、不完全な方法と用語とを用いたとはいえ、交換問題の深い研究を遂げた。少くとも確かに、稀少性の理論すなわち彼らのいわゆる限界利用の理論に経済学者の注意を強く促すのに成功している。今やこの理論は経済学の中に現われて、最も光輝ある未来を予想せられている。私は、この理論から、価値尺度財で表わした商品の価格決定の抽象的理論を導き出した。私は、(一)生産物の価格と土地収入、人的収入、動産収入の同時的決定の理論、(二)純収入率の決定の理論、土地資本、人的資本、動産資本の価格決定の理論、(三)貨幣で表わした価格決定の理論を導き出そうと思う。これらの理論はいずれも抽象的ではあるが、互に関連しているから、組織的な綜合をすれば、現実の説明となり得るであろう(三)。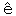 t)と呼ばれる。
t)と呼ばれる。

